自动控制原理课程设计说明书
基于双闭环PID控制的一阶倒立摆控制系统设计
1 任务概述
1.1设计概述
1.2 要完成的设计任务：
2系统建模
2.1 对象模型
2.2 模型建立及封装
3仿真验证
3.1 实验设计
3.2 建立M文件编制绘图子程序
4 双闭环PID控制器设计
4.1内环控制器的设计
4.2外环控制器的设计
5 仿真实验
5.1简化模型
5.2 仿真实验
6 检验系统的鲁棒性
6．1 编写程序求系统性能指标
6.2 改变参数验证控制系统的鲁棒性
7 结论
附录
1 任务概述
1.1设计概述如图1 所示的“一阶倒立摆控制系统”中，通过检测小车位置与摆杆的摆动角，来适当控制驱动电动机拖动力的大小，控制器由一台工业控制计算机(IPC)完成。 图1 一阶倒立摆控制系统 这是一个借助于“SIMULINK封装技术——子系统”，在模型验证的基础上，采用双闭环PID控制方案，实现倒立摆位置伺服控制的数字仿真实验。 1.2 要完成的设计任务：(1)通过理论分析建立对象模型（实际模型），并在原点进行线性化，得到线性化模型；将实际模型和线性化模型作为子系统，并进行封装，将倒立摆的振子质量m和倒摆长度L作为子系统的参数，可以由用户根据需要输入； (2)设计实验，进行模型验证； (3)一阶倒立摆系统为“自不稳定的非最小相位系统”。将系统小车位置作为“外环”，而将摆杆摆角作为“内环”，设计内化与外环的PID控制器； (4)在单位阶跃输入下，进行SIMULINK仿真; (5)编写绘图程序，绘制阶跃响应曲线，并编程求解系统性能指标：最大超调量、调节时间、上升时间； (6)检验系统的鲁棒性：将对象的特性做如下变化后，同样在单位阶跃输入下，检验所设计控制系统的鲁棒性能，列表比较系统的性能指标（最大超调量、调节时间、上升时间）。 倒摆长度L不变，倒立摆的振子质量m从1kg分别改变为1.5kg、2kg、2.5kg、0.8kg、0.5kg； 倒立摆的振子质量m不变，倒摆长度L从0.3m分别改变为0.5m、0.6m、0.2m、0.1m。 2系统建模
2.1 对象模型一阶倒立摆的精确模型的状态方程为： 若只考虑θ在其工作点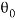 = 0附近的细微变化，这时可以将模型线性化，这时可以近似认为： 一阶倒立摆的简化模型的状态方程为： 2.2 模型建立及封装上边的图是精确模型，下边的是简化模型。 图2 模型验证原理图 2、由状态方程可求得： Fcn:(4/3*u[1]+4/3*m*l*sin(u[3])*power(u[2],2)-10*m*sin(u[3])*cos(u[3]))/(4/3*(1+m)-m*power(cos(u[3]),2)) Fcn1:(cos(u[3])*u[1]+m*l*sin(u[3])*cos(u[3])*power(u[2],2)-10*(1+m)*sin(u[3]))/(m*l*power(cos(u[3]),2)-4/3*l*(1+m)) Fun2:(4*u[1]-30*m*u[3])/(4+m) Fun3:(u[1]-10*(1+m)*u[3])/(m*l-4/3*l*(1+m)) （其中J =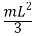 ，小车质量M=1kg，倒摆振子质量m，倒摆长度2L，重力加速度g=10m/ ） 将以上表达式导入函数。 3、如下图框选后选择create subsystem 图3 封装 4、封装之后如下图 图4 子系统建立 5、将精确模型subsystem和简化模型subsystem1组合成以下系统以供验证，注意add的符号是++，不是+-，网上其他的课设都是错的。（输入信号是由阶跃信号合成的脉冲，幅值为0.05，持续时间(step time)为0.1s）。 图5 系统模块封装 6、鼠标右击子系统模块，在模块窗口选项中选择Mask->edit mask，则弹出如下窗口。 图6 添加参数 7、点击左边菜单栏的edit，添加参数m和L，注意prompt中的m和L意思是之后对话框中的提示词，而name中的m和L是要被prompt中输入的值导入的变量，如果name中填错了，那么之后的值将无法导入。 图7 编辑参数 8、在系统模型中，双击子系统模块，则会弹出一个新窗口，在新窗口中可以输入m和L的值，之后将会输入，如图8所示。 图8 输入参数 3仿真验证3.1 实验设计假定使倒立摆在(θ=0，x=0）初始状态下突加微小冲击力作用，则依据经验知，小车将向前移动，摆杆将倒下。 3.2 建立M文件编制绘图子程序图9 绘图子程序 (提示：附录中有子程序方便大家Ctrl+c (＾＿＾)，上边只是为了方便对照)。 - 在系统模型中，双击子系统模块，则会弹出一个新窗口，在新窗口中输入m和l值，点击OK并运行，如图10所示。
图10 输入参数 - 如图设置to file模块的参数，Variable name的名字就是M程序中的函数名，这里如果不是signals的话程序是无法运行的。Save format要选择Array，因为程序是按数组形式调取变量的，没有选择Array的话运行程序会出现“索引超出矩阵维度”的错误。
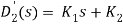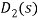图11 to file参数设置 图12 模型验证仿真结果 从中可见，在0.1N的冲击力下，摆杆倒下（θ由零逐步增大）， 小车位置逐渐增加，这一结果符合前述的实验设计，故可以在一定程度上确认该“一阶倒立摆系统”的数学模型是有效的。同时，由图中也可以看出，近似模型在0.8s以前与精确模型非常接近，因此，也可以认为近似模型在一定条件下可以表达原系统模型的性质。 4 双闭环PID控制器设计一级倒立摆系统位置伺服控制系统如图13所示。 图13 一级倒立摆系统位置伺服控制系统方框图 4.1内环控制器的设计内环采用反馈校正进行控制。 图14 内环系统结构图 反馈校正采用PD控制器，设其传递函数为 ，为了抑制干扰，在 前向通道上加上一个比例环节 = K? 控制器参数的整定： 设的增益K = -20，则内环控制系统的闭环传递函数为 令ξ= 0.7 内环控制器的传递函数为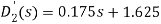： 内环控制系统的闭环传递函数为： 4.2外环控制器的设计外环系统前向通道的传递函数为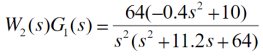： 图12 外环系统结构图 对外环模型进行降阶处理，若忽略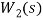 的高次项，则近似为一阶传递函数为： 外环控制器采用PD形式，其传递函数为： 采用单位反馈构成外环反馈通道，则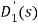 ，则系统的开环传递函数为： 采用基于Bode图法的希望特性设计方法，得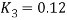 ，τ= 0.87，取τ= 1，则外环控制器的传递函数为 图13 系统仿真结构图 5 仿真实验5.1简化模型- 根据已设计好的PID控制器，可建立图14系统，设置仿真时间为10ms，单击运行。这个仿真是为了便于理解。
-
图14 SIMULINK仿真框图 %将导入到PID.mat中的仿真试验数据读出 load PID.mat t=signals(1,:); q=signals(2,:); x=signals(3,:); %drawing x(t) and thera(t) response signals %画小车位置和摆杆角度的响应曲线 figure(1) hf=line(t,q(:)); grid on xlabel ('Time (s)') axis([0 10 -0.3 1.2]) ht=line(t,x,'color','r'); axis([0 10 -0.3 1.2]) title('\theta(t) and x(t) Response to a step input') gtext('\leftarrow x(t)'),gtext('\theta(t) \uparrow') 执行该程序的结果如图15所示 图15 仿真结果 5.2 仿真实验注意，图中子系统为简化模型而不是精密模型(MMP网上的写的精密模型，调了好久才发现)。 图16 SIMULINK仿真框图 图17系统仿真结果图 6 检验系统的鲁棒性检验系统的鲁棒性：将对象的特性做如下变化后，同样在单位阶跃输入下，检验所设计控制系统的鲁棒性能，列表比较系统的性能指标（最大超调量、调节时间、上升时间）。 6．1 编写程序求系统性能指标 新建pid.m文件，输入以下命令并保存 load PID.mat clc t=signals(1,:); x=signals(2,:); q=signals(3,:); figure(1) hf=line(t,q(:)); grid on axis([0 10 -0.3 1.2]) ht=line(t,x,'color','r'); r=size(signals); e=r(1,2); C=x(1,e); %得到系统终值 y_max_overshoot=100*(max(x)-C)/C %超调量计算 r1=1; while (x(r1)<0.1*C) r1=r1+1; end r2=1; while (x(r2)<0.9*C) r2=r2+1; end x_rise_time=t(r2)-t(r1) %上升时间计算 s=length(t); while x(s)>0.98*C&&x(s)<1.02*C s=s-1; end x_settling_time=t(s) %调整时间计算 C1=q(1,e); [max_y,k]=max(q); q_max_overshoot=max(q)-C1 %超调量计算 q_rise_time=t(k) %上升时间计算 s=length(t); while q(s)>-0.02&&q(s)<0.02 s=s-1; end q_settling_time=t(s) %调整时间计算 6.2 改变参数验证控制系统的鲁棒性 倒摆长度L不变，倒立摆的振子质量m从1kg分别改变为1.5kg、2kg、2.5kg、0.8kg、0.5kg；倒立摆的振子质量m 不变，倒摆长度L 从0.3m 分别改变为0.5m、0.6m、0.2m、0.1m。在单位阶跃输入下，检验所设计系统的鲁棒性 。 - 改变输入参数并运行，再运行pid.m文件，得到响应曲线及性能指标，记录表1
图18 改变输入参数 表1 性能坐标比较 图19改变倒立杆质量和长度时系统仿真结果 7 结论结论： 1、原系统在0.1N的冲击力下，摆杆倒下（θ由零逐步增大）， 小车位置逐渐增加，这一结果符合前述的实验设计，故可以在一定程度上确认该“一阶倒立摆系统”的数学模型是有效的。验证实验中，通过精确模型与简化模型比较，从图中可以看出，0.8s以前是非常接近，因此，也可以认为近似模型在一定条件下可以表达原系统模型的性质。 2、经过双闭环PID 控制的系统，能跟随给定并稳定下来，且θ终值为0使摆杆不倒。说明PID控制有效。 3、改变倒立摆的摆杆质量m和长度L。从图11中可以看出，在参数变化的一定范围内系统保持稳定，控制系统具有一定的鲁棒性。 附录- q=signals(4,: ); %读取精确模型中倒摆摆角信号
- xx=signals(5,: ); %读取简化模型中的小车位置信号
- qq=signals(6,: ); %读取简化模型中倒立摆摆角信号
- figure(1) %定义第一个图形
- hf=line(t,f(:)); %连接时间-作用力曲线
- grid on;
- xlabel('Time(s)') %定义横坐标
- ylabel('Force(N)') %定义纵坐标
- axis([0 1 0 0.12]) %定义坐标范围
- axet=axes('Position',get(gca,'Position'),...
- 'XAxisLocation','bottom',...
- 'YAxisLocation','right','color','none',...
- 'XColor','k','YColor','k');
- %定义曲线属性
- ht=line(t,x,'color','r','parent',axet);
- %连接时间-小车位置曲线
- ht=line(t,xx,'color','r','parent',axet);
- %连接时间-小车速度曲线
- ylabel('Evolution of the xposition(m)') %定义坐标名称
- axis([0 1 0 0.1]) %定义坐标范围
- title('Response x and x''in meter to a f(t) pulse of 0.1 N' )
- %定义曲线标题名称
- gtext ('\leftarrow f (t)'),gtext ('x (t) \rightarrow') , gtext (' \leftarrow x''(t)')
- figure (2)
- hf=line(t,f(:));
- grid on
- xlabel('Time')
- ylabel('Force(N)')
- axet=axes('Position',get(gca,'Position'),...
- 'XAxisLocation','bottom',...
- 'YAxisLocation','right','color','none',...
- 'XColor','k','YColor','k');
- ht=line(t,q,'color','r','parent',axet);
- ht=line(t,qq,'color','r','parent',axet);
- ylabel('Angle evolution (rad)')
- axis([0 1 -0.3 0])
- title('Response \theta(t)and \theta'' in rad to a f(t) pulse of 0.1 N' )
以上图文的Word格式文档下载(内容和本网页上的一模一样,方便大家保存):：源文件:无
| 
进行近似处理，则
