标题: music算法仿真，信号频率估计详解 [打印本页]
作者: 480601002    时间: 2018-8-7 09:33
标题: music算法仿真，信号频率估计详解
里面有源文件和仿真结果，与分析

信号频率估计

信号频率估计是信息科学在信号处理领域的一个重要的组成部分，指的是通过对信号采样值的计算和变换，估计出淹没于噪声中的信号频率。按照信号的平稳性差异，可将频率估计方法分为平稳信号频率估计与非平稳信号频率估计。

平稳信号频率估计始于1822年，傅里叶提出谐波分析理论，奠定了信号分析和功率谱估计理论基础。在19实际末，Schuster提出周期图概念，至今沿用。在1958年，Blackman和Tukey提出自相关谱估计，简称BT法。以上几种方法为信号频率估计经典法。经典法的缺点是分辨力低（为1/N，N为数据长度），提高分辨力需增加数据长度N，从而增加运算时间。对此，提出了修正平均周期图法（Welch法）、Bartlett法等。

在60年代末70年代初，科学家们提出使用现代法来进行信号的频率估计，以提高频率分辨率。现代法分为两类：参数估计法，非参模型法。参数估计法包括：自回归（AR）模型，滑动平均（MA）模型，自回归滑动平均（ARMA）模型。参数估计法具有较好的频率分辨能力，运算速度较快，但性能受参数的选取等因素的影响。非参数模型法包括：最大似然法，最小方差无失真法（MVDR），多信号分类法（MUSIC），子空间旋转不定法（ESPRIT）。

对于非平稳信号来说，瞬时频率随时间变化，时频分布能够更准确的分析信号的时变本质，让分析精确到具体时间和特定的频率上，使用的方法有Gabor变换，短时傅里叶变换，小波变换，S变换，Hilbert-Huang变换等。

下面具体介绍不同的信号频率估计方法。

1、周期图法（Periodogram）

周期图法通过计算采样信号的FFT，获得离散点的幅度，然后取其幅频特性的平方并除以序列长度N。

由于序列x(n)的离散傅里叶变换X(ejw)具有周期性，因而这种功率谱也具有周期性，被称为周期图。因其直接观察数据的傅氏变换，又被称为直接法。周期图是信号功率谱的一个有偏估值，随着所取信号序列的长度的不同，所得到的周期图也不同。应用时，要在方差、偏差、分辨率之间进行折中选择。

2、自相关函数法（BT法）

设uN(n)为u(n)的N个观测值，则u(n)的自相关函数估计值为
根据维纳-辛钦（Wiener-Khintchine）定理，对上式求傅里叶变换
因为上式是通过自相关函数间接得到的，又称为间接法。因为

当m和N都比较大时，计算量很大。

接下来介绍现代法中的参数估计法。

参数估计法的基本思路：1、参数模型假设研究过程是由一个输入序列u(N)激励一个线性系统H(z)的输出。2、由假设参数模型的输出x(n)或其自相关函数来估计H(z)的参数。3、由H(z)的参数估计x(n)的功率谱。所以参数模型功率谱的求解有两步：1、H(z)模型参数估计2、依据模型参数求功率谱。

3、AR模型法

x(n)的功率谱可表示为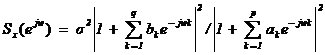

是激励白噪声的方差，Sx(ejw)为功率谱密度，ak和bk为模型参数。若式中参数b1,b2,…,bq全为0，则上式变为即为AR模型。
AR模型又称为自回归模型，是一个全极点模型。该模型现在的输出是现在的输入和过去p个输出的加权和：，式中u(n)为白噪声信号，p为AR模型的阶数。对上式求z变换，得到系统函数：

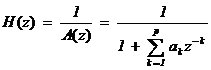
由随机信号通过线性系统理论知输出序列的功率谱：

，

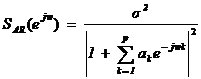式中，为白噪声序列方差。AR模型估计中，由于隐含自相关函数的外推，而使分辨率大大提高；从而观测数据的多少对分辨率影响不大，但对估计误差会有影响，数据越多，估计误差越小。AR模型中阶数p越低，功率谱分辨率降低，但谱的平滑性变好，估计误差降低。

4、ARMA模型法
ARMA模型是既有零点，又有极点的模型。ARMA(p，q)的差分方程如下，其中u(n-k)是零均值，方差为的白噪声，p，q分别为自回归（AR）和滑动平均（MA）的阶数。由AR模型得到，对已知数据uN(n)，经过，输出y(n)近似于一个MA(q)过程，求出和输入噪声方差的估计，从而实现ARMA(p，q)模型的参数估计。得到
5、最大似然法（ML法）

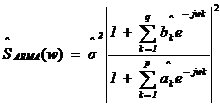
最大似然法频率估计是通过求解似然函数的最大值来进行频率估计，此法对信噪比门限要求较低，不需要事先对噪声进行学习，应用简便，是最准确的频率估计方法；但在求解最大似然函数最大值时要求解一个高度非线性化的方程，计算量非常大，有时甚至无法求解，不适用于实时计算。

设信号表示为，其中，a(t)已知；相位是在上均匀分布的随机变量；频率w是待估计的信号参量。接收信号表示为，其中，n(t)是均值为零的高斯白噪声。当频率w为待估计量时，有

其中，
因为，所以
，
式中。令，则有，这样，似然函数
将对在上求统计平均，得

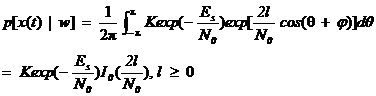
由p[x(t)|w]对w求极大值就能得到频率w的最大似然估计量。

6、多信号分类法（MUSIC算法）

MUSIC算法利用信号子空间和噪声子空间的正交性，构造空间谱函数，通过谱峰搜索，估计信号频率。

根据观测样本值x(0)，x(1)，…，x(N-1)，估计自相关矩阵；对进行特征分解，得到(M-K)个最小特征值对应的特征向量，构造矩阵G；在

[-π，π]内改变w，计算SMUSIC(w)，峰值位置就是信号频率的估计值。

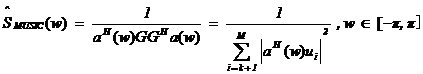
MUSIC算法是空间谱估计方法中极为重要的一种，分辨率高，对信号个数、噪声干扰强度、相干关系等可以进行渐近无偏估计，在噪声子空间大于信号子空间时，MUSIC算法有非常好的性能。但其需要在整个频域内进行谱峰搜索，实时性较差。

7、旋转不变子空间算法（ESPRIT算法）

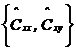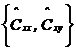ESPRIT算法是基于旋转不变技术的信号参数估计方法。首先，根据观测样本值x(0)，x(1)，…，x(N-1)，估计相关矩阵；其次，对进行特征分解，计算得到最小特征值；之后，构造矩阵对，其中；然后对进行广义特征分解，最接近单位圆的K个广义特征值的相位给出了信号频率的估
计。

ESPRIT算法具有较高的估计精度，无需像MUSIC算法一样进行谱峰搜索，而是直接解出估计的信号频率。但是ESPRIT算法需进行两次特征值分解，计算量较大。

8、非平稳信号频率估计方法

对于非平稳信号，不能简单的使用平稳信号的估计方法，必须考虑时变因素。人们希望找到一个二维函数，既能反映信号的频率内容，也能反映出该频率内容随时间变化的规律。其中最典型的是以Cohen类为代表的双线性时频分布，此分布可表示为

式中,是一个二维窗函数，给定不同的窗函数可以得到不同的时频分布。
若，式中w是一个一维的窗函数，上式可以简化为如下的谱图
式中，称为信号x(t)的短时傅里叶变换，它
反映了信号的频谱随时间和频率的分布。

短时傅里叶变换，它将分段加窗后的信号视为平稳信号，然后利用傅里叶变换进行分析，属于线性变换，对地信噪比下的多分量信号有良好的分析能力，但是其时频分辨率较低，存在窗口效应。

下面对MUSIC算法进行仿真说明，设被测量频率为0.4Hz。

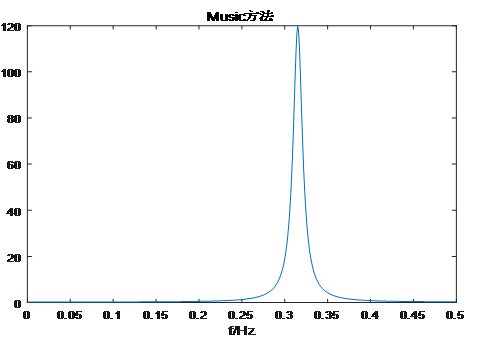
Snr=-20时,解出f=0.315Hz，实际f=0.400Hz，相对误差15.25%

Snr=-15时，解出f=0.412Hz，相对误差7.5%

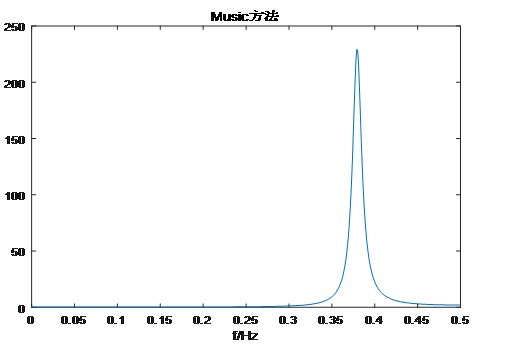
Snr=-10时，解出f=0.379Hz，相对误差5.25%

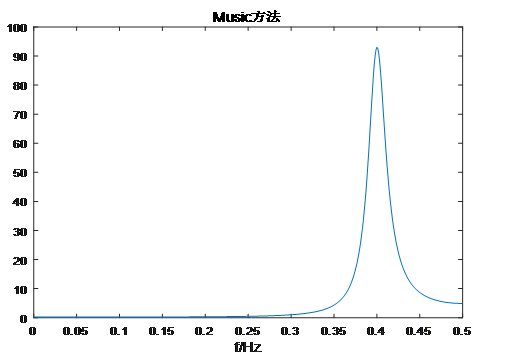
Snr=-5时，解出f=0.3920Hz，相对误差2%

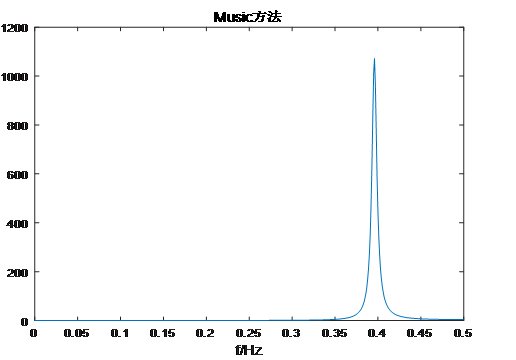
Snr=0时，解出f=0.3990Hz，相对误差0.5%

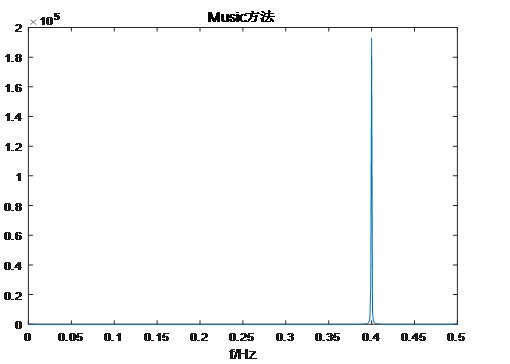
Snr=5时，解出f=0.400Hz，相对误差0%

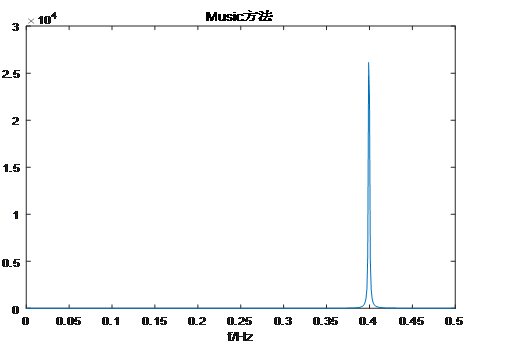
Snr=10时，解出f=0.400Hz，相对误差0%。

在不同信噪比的情况下，计算1000组数据的相对误差。

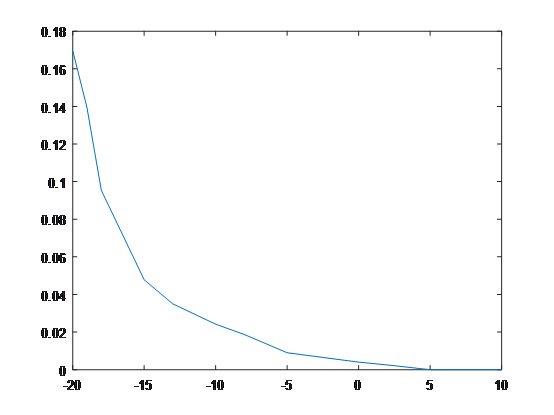
信噪比与相对误差的关系，横轴为信噪比，竖轴为相对误差。


完整的Word格式文档51黑下载地址：

信号频率估计.docx (160.59 KB, 下载次数: 57)


作者: jin11408    时间: 2019-11-12 22:04
谢谢分享
作者: 3392857307    时间: 2020-9-22 18:30
里面没有程序源文件，不要下载



欢迎光临 (http://www.51hei.com/bbs/) Powered by Discuz! X3.1