标题: 基于双闭环PID控制的一阶倒立摆控制系统课程设计 [打印本页]
作者: LJBB    时间: 2018-10-23 15:40
标题: 基于双闭环PID控制的一阶倒立摆控制系统课程设计
自动控制原理课程设计-基于双闭环PID控制的一阶倒立摆控制系统设计
倒立摆是一个非线性、不稳定系统,经常作为研究比较不同控制方法的典型例子。设计一个倒立摆的控制系统，使倒立摆这样一个不稳定的被控对象通过引入适当的控制策略使之成为一个能够满足各种性能指标的稳定系统。
倒立摆的设计要求是使摆杆尽快地达到一个平衡位置，并且使之没有大的振荡和过大的角度和速度。当摆杆到达期望的位置后，系统能克服随机扰动而保持稳定的位置。实验参数自己选定，但要合理符合实际情况，控制方式为双PID控制，并利用 MATLAB进行仿真，并用simulink对相应的模块进行仿真。
     倒立摆控制系统的工作原理是：由轴角编码器测得小车的位置和摆杆相对垂直方向的角度，作为系统的两个输出量被反馈至控制计算机。计算机根据一定的控制算法，计算出空置量，并转化为相应的电压信号提供给驱动电路，以驱动直流力矩电机的运动，从而通过牵引机构带动小车的移动来控制摆杆和保持平衡。
首先画出一阶倒立摆控制系统的原理方框图
一阶倒立摆控制系统示意图如图所示：
分析工作原理，可以得出一阶倒立摆系统原理方框图：
一阶倒立摆控制系统动态结构图
下面的工作是根据结构框图，分析和解决各个环节的传递函数！

1.一阶倒立摆建模

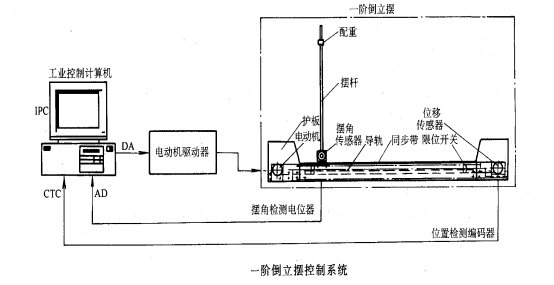
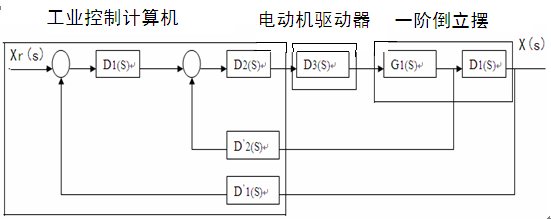
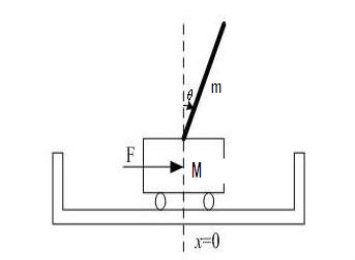
在忽略了空气流动阻力，以及各种摩擦之后，可将倒立摆系统抽象成小车和匀质杆组成的系统，如下图所示，其中：   

M：小车质量  

m：为摆杆质量   

J：为摆杆惯量   

F：加在小车上的力  

x：小车位置  

θ：摆杆与垂直向上方向的夹角  

l ：摆杆转动轴心到杆质心的长度

根据牛顿运动定律以及刚体运动规律，可知：

   

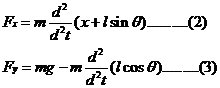
得

（3）小车水平方向上的运动为

联列上述4个方程，可以得出

一阶倒立精确气模型：

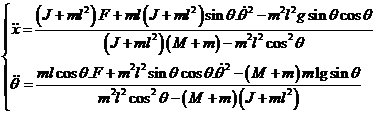
式中J为摆杆的转动惯量：

若只考虑θ在其工作点附近θ0=0附近（）的细微变化，则可以近似认为：

                             

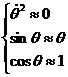
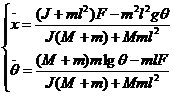
若取小车质量M=2kg,摆杆质量m=1kg,摆杆长度2l =1m,重力加速度取g=,则可以得

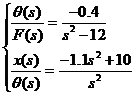一阶倒立摆简化模型：

            拉氏变换

即      G1(s)= ;       G2(s)=

一阶倒立摆环节问题解决！

2.电动机驱动器

选用日本松下电工MSMA021型小惯量交流伺服电动机，其有关参数如下：

驱动电压：U=0~100V            额定功率：PN=200W

额定转速：n=3000r/min         转动惯量：J=3×10-6kg.m2

额定转矩：TN=0.64Nm           最大转矩：TM=1.91Nm

电磁时间常数：Tl=0.001s       电机时间常数：TM=0.003s

经传动机构变速后输出的拖动力为：F=0~16N；与其配套的驱动器为：MSDA021A1A，控制电压：UDA=0~±10V。

若忽略电动机的空载转矩和系统摩擦，就可以认为驱动器和机械传动装置均为纯比例环节，并假设这两个环节的增益分别为Kd和Km。

            

   

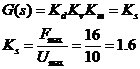
即D3(s)=1.6

电动机驱动器部分问题解决！


3.双闭环PID控制器设计

剩下的问题就是如何确定控制器的结构和参数。

（一）内环控制器的设计




其中，Ks=1.6为伺服电动机与减速机构的等效模型

1.控制器的选择

内环系统未校正时的传递函数为

对于内环反馈控制器D2(s)可有PD，PI，PID三种可能的结构形式，怎么选取呢？这里，不妨采用绘制各种控制器结构下“系统根轨迹”的办法加以分析比较，从之选出一种比较适合的控制器结构。

各种控制器的开环传函的传递函数分别为：

在MATLAB下输入以下程序用“凑试”的方法画根轨迹图：
num=[分子];
den=[分母];
xlabel('Real Axis');
ylabel('Imag Axis');
axis([横、纵坐标范围]);
title('Root Locus');
grid;
rlocus(num,den)
下图为各种控制器下的系统根轨迹。
                  （a） PD                （b） PD

                 （c）PI                     d） PID

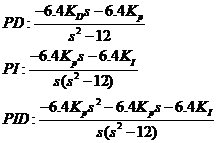
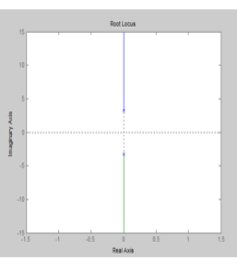
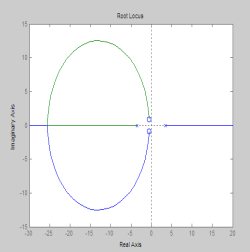
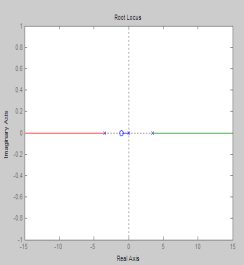
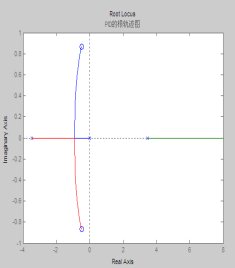
    从根轨迹不难发现，采用PD结构的反馈控制器，结构简单且可保证闭环系统的稳定。所以，选定反馈控制器的结构为PD形式的控制器。

2.控制器参数的选定

首先暂定K=-20。这样可以求出内环的传递函数为：

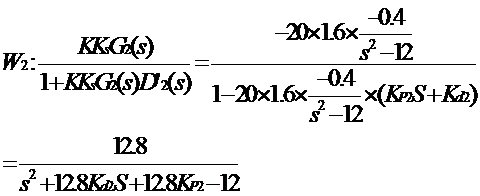
注释：工程上常用阻尼比=0.707作为二阶系统最优解！

3.系统内环的simulink仿真及结果

仿真结果为：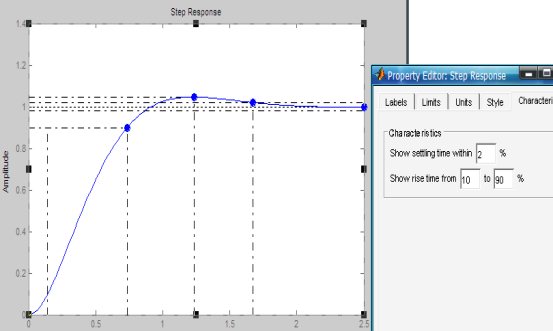




（二）外环控制器的设计

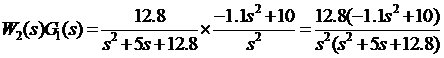
可见，系统开环传递函数可视为一个高阶（4阶）且带有不稳定零点的“非最小相位系统”，为了便于设计，需要首先对系统进行一些简化处理（否则，不便利用经典控制理论与方法对它进行设计）。

１.系统外环模型的降阶

（1）对内环等效闭环传递函数的近似处理

将高次项忽略，有

近似条件可由频率特性导出，即

由（2）得：           

          

            

由（3）得：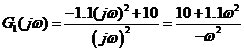

由（4）得：           

    ，所以，有

近似条件为：

２.控制器设计

设加入的调节器为   ，同时，为使系统有较好的跟随性能，采用单位反馈来构成外环反馈通道，如图所示：

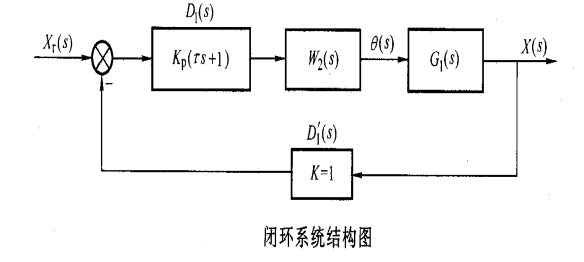
取               

再由“典型Ⅱ型”系统Bode图特性（ ）知：

   

３.用simulink对小车的位置在阶跃信号输入下的响应进行仿真：

系统框图为

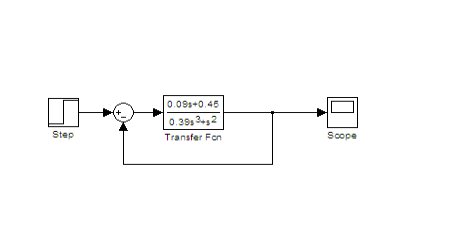
仿真结果：

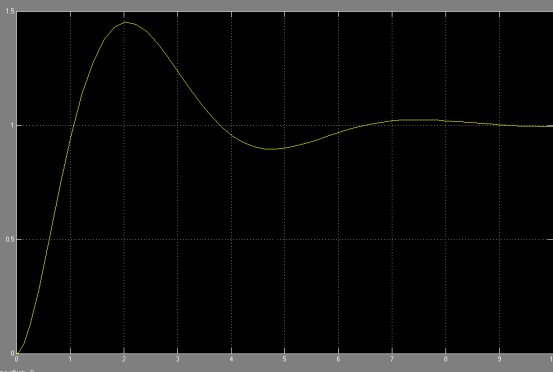
倒立摆位置在阶跃信号下的响应


3.系统的simulink仿真

连接图如下：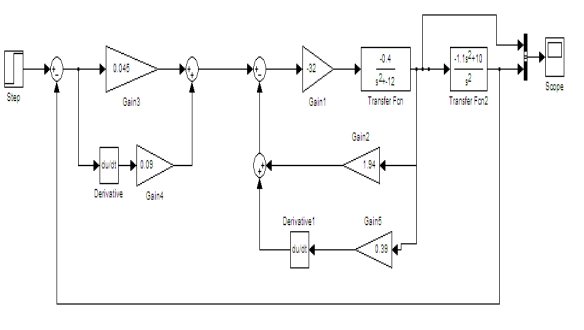

仿真结果为：

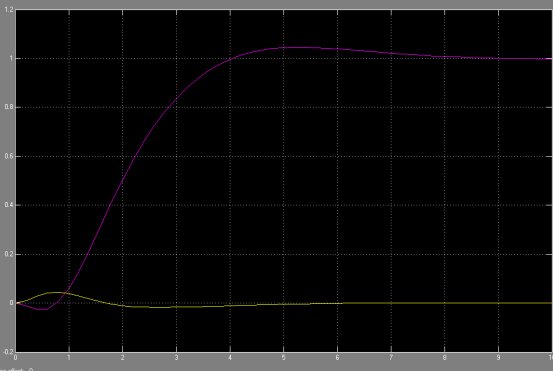
倒立摆在阶跃信号下摆杆和小车位置的响应

从图中可以看出建立的一阶倒立摆控制系统在matlab中能够实现倒立摆的要求，能通过电动机牵引机构带动小车的移动来控制摆杆和保持平衡。

为了进一步验证在不同摆杆下的，该一阶倒立摆控制系统是否还具有鲁棒特性，分别取摆杆不同的质量和摆长，进行simulink仿真！


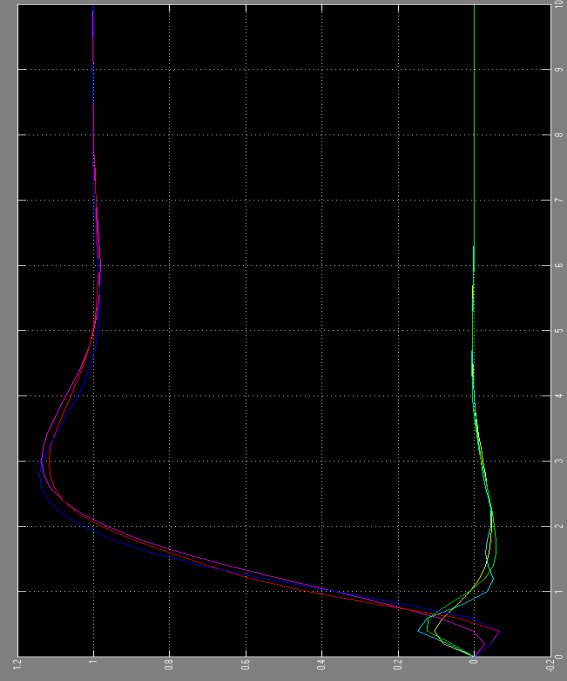
由图可知，建立的一阶倒立摆模型在不同摆长下能实现要求。但摆长不能过长！同理，建立的一阶倒立摆模型在不同质量的摆杆下能也实现要求，但同样不能过重！

五、课程设计心得

1、通过实验了解了一阶倒立摆是的非线性、不确定性、不稳定系统和约束限制,同时倒立摆也是经常作为研究比较不同控制方法的典型例子。

2、对一阶倒立摆控制系统的研究使我了解到倒立摆还有二阶倒立摆、三阶倒立摆，甚至四阶倒立摆，同时还涉及到起摆的问题！增加了了倒立摆研究的兴趣！

3、建立的一阶倒立摆控制系统忽略了许多因素，应用一些简化处理，即建立的只是一阶倒立摆控制系统的简化模型。当摆杆的质量和摆长超过一定范围，系统失效,所以该系统有待改进！



完整的Word格式文档51黑下载地址：

一级倒立摆控制系统设计.doc (511 KB, 下载次数: 60)


作者: Fudan    时间: 2018-11-3 01:12
大佬，我没有足够的黑笔下载您的文档。
作者: Fudan    时间: 2018-11-3 01:12
您实惠，用百度网盘分享一下资料。
作者: daodaoisgod001    时间: 2020-4-13 14:58
太棒了我找到了



欢迎光临 (http://www.51hei.com/bbs/) Powered by Discuz! X3.1