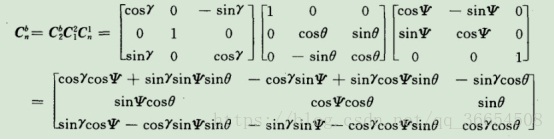

这个先用一句话囊括一下:不同的坐标值对应空间同一个位置,多个坐标值对应同一个位置的不一致性是造成死锁的根源。
然后就举个例子:
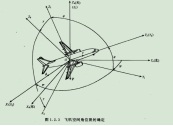
假如我们有一个望远镜和一个用来放望远镜的三脚架,(我们将)三脚架放在地面上,使支撑望远镜的三脚架的顶部是平行于地平面(参考平面)的,以便使得竖向的旋转轴(记为 x 轴)是完全地垂直于地平面的。现在,我们就可以将望远镜饶 x 轴旋转 360 度,从而观察(以望远镜为中心的)水平包围圈的所有方向。通常将正北朝向方位角度记为 0 度方位角。第二个坐标轴,即平行于地平面的横向的坐标轴(记为 y 轴)使得望远镜可以饶着它上下旋转,通常将地平面朝向的仰角记为 0 度,这样,望远镜可以向上仰+90 度指向天顶,或者向下-90 度指向脚底。好了,万事俱备。现在,天空中(包括地面上)的每个点只需要唯一的一对 x 和 y 度数就可以确定。比如 x=90 度,y=45 度指向的点是位于正东方向的半天空上。
现在,看看万向节死锁是怎么发生的。一次,我们探测到有一个飞行器贴地飞行,位于望远镜的正东方向(x=90 度,y=10 度),朝着我们直飞过来,我们跟踪它。飞行器飞行方向是保持 x 轴角度 90 度不变,而 y 向的角度在慢慢增大。随着飞行器的临近,y 轴角增长的越来越快且当 y 向的角度达到 90 度时(即将超越),突然它急转弯朝南飞去。这时,我们发现我们不能将望远镜朝向南方,因为此时 y 向已经是 90 度,造成我们失去跟踪目标。这就是万向节死锁!
为什么说不能将望远镜朝向南方呢,让我们看看坐标变化,从开始的(x=90 度,y=10度)到(x=90 度,y=90 度),这个过程没有问题,望远镜慢慢转动跟踪飞行器。当飞行器到达(x=90 度,y=90 度)后,坐标突然变成(x=180 度,y=90 度)(因为朝南),x 由 90突变成 180 度,所以望远镜需要饶垂直轴向 x 轴旋转 180-90=90 度以便追上飞行器,但此时,望远镜已经是平行于 x 轴,我们知道饶平行于自身的中轴线的的旋转改变不了朝向,就象拧螺丝一样,螺丝头的指向不变。所以望远镜的指向还是天顶。而后由于飞行器飞远,坐标变成(x=180 度,y<90 度)时,y 向角减小,望远镜只能又转回到正东指向,望’器’兴叹。这说明用 x,y 旋转角(又称欧拉角)来定向物体有时并不能按照你想像的那样工作,象上面的例子中从(x=90 度,y=10 度)到(x=90 度,y=90 度),按照欧拉角旋转确实可以正确地定向,但从(x=90 度,y=90 度)到(x=180 度,y=90 度),再到(x=180 度,y<90 度),按照欧拉角旋转后的定向并非正确。我的理解是坐标值的变化和飞行器空间的位置变化一一对应,但是从(x=90 度,y=90 度)到(x=180 度,y=90 度),再到(x=180 度,y<90度)这个变化,飞行器位置是连续的变化,但坐标值的变化却不是连续的(从 90 突变到180),其原因在于(x=90 度,y=90 度)和(x=180 度,y=90 度)甚至和(x=任意度,y=90 度)这些不同的坐标值对应空间同一个位置。。。
同样对于2维或者3维都是一样的(例子是抄的、、、)
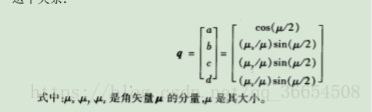
刚刚说过可以用方向余弦表示矢量在坐标轴的位置,也就是说可以得出载体坐标轴xyz分别与参考坐标轴XYZ的方向余弦。形成余弦矩阵
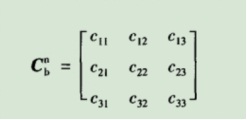
第i行、第j列的元素表示参考坐标系i轴和载体坐标系j轴夹角的余弦。
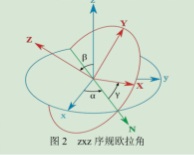
回过头来再比较一下欧拉角和方向余弦其实没有什么区别,就是用方向余弦表示欧拉角。这两个的坐标变换在《惯性导航》里面都有相应的推导。(此处略)
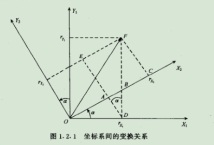
三个坐标轴的变换用矩阵表示就是这样

此处再说明一下矩阵的意义。
C 表示坐标系1到坐标系2的变换矩阵
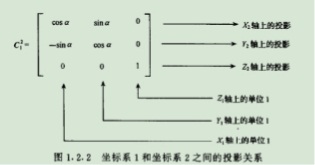
在线性代数中两复杂矩阵的变化可通过有限的矩阵相乘的运算获得,当然在坐标系中同样也适用。两坐标系任何复杂的角位置关系都可以看做有限次基本旋转的组合