标题: 通信原理Matlab求积分和微分 代码 [打印本页]
作者: 败笔 时间: 2025-6-13 00:58
标题: 通信原理Matlab求积分和微分 代码
这是我的答案(虽然我看不懂)
无论是积分和微分,都有符号和数值两种操作,符号操作是计算精确解析式和相应的精确值:
符号:
sysm x t---->定义自变量
int(f,x) ---->求f关于x的不定积分
int(g,t) ---->求g关于t的不定积分
int(f,x,a,b) ---->求f关于x在[a,b]上的定积分
diff(f,x,n) ---->求f关于x的n阶导数
数值方法:
数值微分:
#用函数值的差分除以自变量的差分(只要步长足够小,就足够精确)
diff(y). /diff(x),但是会比原函数的维度少一位
数值积分:
#数值积分可以基于不同的积分准则,如:中点法则、梯形法则、辛普森法则等,因此也有不同的函数
1. 基于自适应 Simpson 积分法计算数值积分(不推荐)
如:计算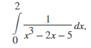 ,可以:
,可以: 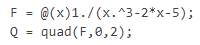 ,F为待计算函数句柄(匿名)
,F为待计算函数句柄(匿名)2. 基于自适应Gauss-Lobatto方法(不推荐)
和quad一样的用法,把quad换成quadl
3. 基于高斯-勒让德积分方法(和integral的积分方法基本相同)
和quad一样的用法,把quad换成quadgk
4. 基于全局自适应积分法(推荐)
与quad一样的用法,将quad换成integral
5. 基于梯形积分法
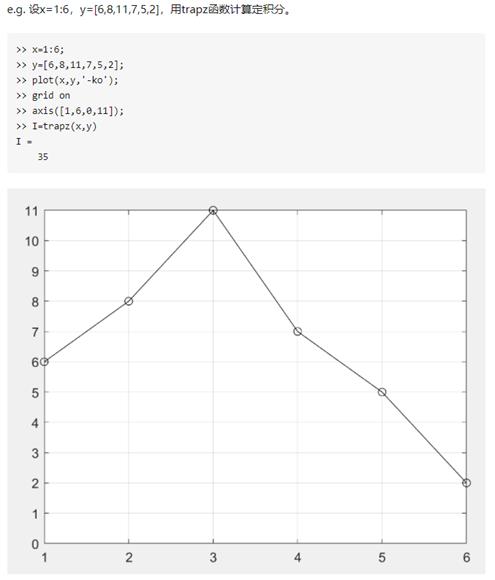
- %研究各种信号的抗噪声性能(直接引用前几个文件的基础代码)
- clear all;
- close all;
- %tips: biterr函数、randn函数
- %-------------------------ASK---------------------------
- %----原始信号码元参数----
- Tb = 1; %码元长度
- fs = 100; %采样频率
- dt = 1/fs; %采样时间间隔
- N = 1e5; %码元数量,数量大,便于统计,避免较少的码元数带来的偶然性
- t = 0:dt:(N*fs-1)*dt; %时域范围
- %----载波参数----
- Ac = 1; %载波幅度
- fc = 30; %载波频率
- phi = 0; %初始相位
- %----产生原始的二进制码元----
- sr = (sign(randn(1,N))+1)/2; %原始信息序列
- sr_conv = zeropad(sr,fs);
- nrz = ones(1,fs); %单个NRZ波形
- data = conv(sr_conv,nrz);
- data = data(1:length(t));
- %----产生ASK信号----
- carrier = cos(2*pi*fc*t);
- ask = data.*carrier;
-
- %----匹配滤波----
- r_db = 0:15; %信噪比-dB
- Eb = Tb*Ac*Ac/2; %单个比特的信号功率(J/bit)
- pe = zeros(1,length(r_db));
- pe_ideal = zeros(1,length(r_db));
- for i=1:length(r_db)
- r = 10^(r_db(i)/10);
- n0 = Eb/r; %单边噪声功率谱密度
- delta = n0/2*fs; %噪声功率
- n = sqrt(delta)*randn(1,length(ask)); %噪声信号
- % reciv = awgn(ask,r_db(i)); %也可以这样
- reciv = ask+n; %接收信号
-
- %匹配滤波器
- t1 = 0:dt:Tb-dt;
- h = cos(2*pi*fc*t1);
-
- %滤波
- recov_signal = conv(reciv,h)*dt;
-
- %包络检波
- t2 = 0:dt:(length(recov_signal)-1)*dt;
- z = hilbert(recov_signal); %z为解析信号
- z1 = z.*exp(-sqrt(-1)*2*pi*fc*t2); %z1为复包络
- envlp = abs(z1);
- % subplot(2,1,1);
- % plot(t,data);
- % subplot(2,1,2);
- % plot(t2,recov_signal);
-
- %判决
- recov_sym = zeros(1,N);
- Vth = Ac/4; %判决门限,余弦信号卷积之后,高度会下降一半,故用Ac/4
- for j=1:N
- if envlp(j*Tb/dt) > Vth
- recov_sym(j)=1;
- else
- recov_sym(j)=0;
- end
- end
- [err_num,err_pro] = biterr(sr,recov_sym); %计算误码个数和误码率
- pe(i)=err_pro;
- pe_ideal(i) = 0.5*erfc(sqrt(0.25*r));
- %pe_ideal(i) = 0.5*exp(-0.25*r);
- end
- figure();
- semilogy(r_db,pe,'-*');
- hold on;
- semilogy(r_db,pe_ideal);
- legend('实际误码率','理论误码率');
- grid on;
- % 评估二进制单极性和双极性基带系统的抗噪性能
- SNR_dB = 0:0.05:10;
- scal = 10.^(SNR_dB/10); %信噪比的比例形式
- A_over_sigma = sqrt(scal)*sqrt(2);
- double = 0.5*erfc(sqrt(scal));
- single = 0.5*erfc(0.5*sqrt(scal));
- figure('NumberTitle', 'off', 'Name','相同抽样电平下两种数字基带系统的抗噪声能力');
- semilogy(A_over_sigma,double);
- hold on;
- semilogy(A_over_sigma,single);
- xlabel('抽样电平/噪声均方值');
- ylabel('系统误码率Pe');
- grid on;
- legend('双极性','单极性');
- %tips:数字基带系统的抗噪性能(不考虑码间干扰,受噪声引起的误码率)与信号码元抽样电平的值与噪声均方根值(功率开方,即高斯噪声的方差开方)之比有关
- %如果是理想的方波码元,功率为A
- %第4-5行其实是验证了两种编码方式:相同的电平值A和噪声均方值下不同的抗噪表现,而不是相同的信噪比条件下,因为如果两个信号的SNR相同,则两个信号的电平值也不同
- %----验证相同SNR下不同系统的抗噪性能(此时两种信号的电平值也不同)-----
- double_2 = 0.5*erfc(sqrt(scal)/sqrt(2));
- single_2 = 0.5*erfc(sqrt(scal)/2);
- figure('NumberTitle', 'off', 'Name','相同SNR下两种数字基带系统的抗噪声能力');
- semilogy(SNR_dB,double_2);
- hold on;
- semilogy(SNR_dB,single_2);
- xlabel('SNR(Eb/N0)-dB');
- ylabel('系统误码率Pe');
- grid on;
- legend('双极性','单极性');
代码下载:
 Communication-Matlab-main.7z
(71.93 KB, 下载次数: 0)
Communication-Matlab-main.7z
(71.93 KB, 下载次数: 0)
| 欢迎光临 (http://www.51hei.com/bbs/) |
Powered by Discuz! X3.1 |



 Communication-Matlab-main.7z
(71.93 KB, 下载次数: 0)
Communication-Matlab-main.7z
(71.93 KB, 下载次数: 0)