一道简单几何题的解法 -

标题: 一道简单几何题的解法 [打印本页]

作者: 51黑er 时间: 2015-11-2 13:45
标题: 一道简单几何题的解法

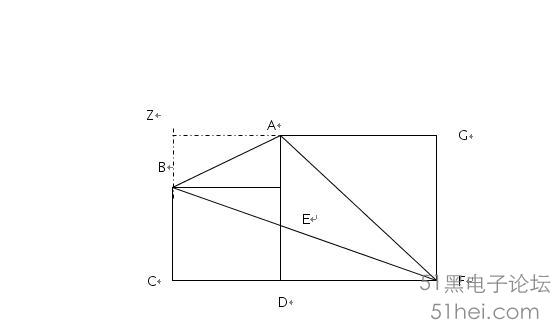
如图，上图左边为小正方形边长为3，右面大正方形为5.求三角形ABF的面积。

解：延长GA、CB交与Z点。

则构成矩形ZCFG。设小正方形边长为x

三角形ABF面积等于矩形ZCFG面积减去三角形ZBA、AGF、BCF的面积。

面积ABF=(5+x)*5-(5+x)*x/2-(5-x)*x/2-5*5/2

=25+5*x-5/2*x-x*x/2-5*x/2+x*x/2-25/2

=25/2

注意，由于削去了x的所有项只剩常数项，所以结果和小正方形边长无关。

其实题目结果可以这样理解：

如图，正方形ABCD。AC为对角线，做BF直线，平行于AC。这样FBC角度为135=90+45度。在FB上任取一点E，则三角形ACE的面积为底*高，为AC*H，H为平行线间距=BO.

因此三角形面积和E点位置无关，即使BE>AC。

由于角度EBA=45度，因此，过E点总可以做出一个小正方形贴紧大正方形。郭天宇，理解了吗？其实都等于三角形ABC的面积，也就是矩形ABCD的面积的一半，即S=5*5/2=25/2.

欢迎光临 (http://www.51hei.com/bbs/)