标题: 最小拍控制系统课程设计报告(论文)下载 [打印本页]
作者: 啊大王    时间: 2017-7-24 11:08
标题: 最小拍控制系统课程设计报告(论文)下载
桂林航天工业学院
课程设计报告
系（部）电子信息与自动化学院 专业班级14自动化三班
学生姓名：　黄*义　　　学   号： 2222222222222
设计题目：　最小拍控制系统
完成日期2017 年　6　月　13　日　　　　


指导教师评语：

成绩（五级记分制）：
指导教师（签字）：_____________________

桂林航天工业学院课程设计任务书
设计题目：最小拍控制系统
学生姓名
黄发义
课程名称
最小拍控制系统
专业班级
14自动化三班
地    点
巡天408
起止时间
2017.06.12-2017.06.15
设计内容
最小拍控制系统设计

设计参数
最小控制系统设计选择一个被控对象，整定参数后阶跃响应小于10%

设计进度
已经完成


设计成果
  • 设计说明书  2、设计计算书 3、仿真分析结果  4、系统原理图
参考资料
【1】胡寿松  自动控制原理    科学出版社
【2】李元春  计算机控制系统  高等教育出版社
【3】何衍庆等 控制系统分析、设计和应用 化学工业出版社

说明
1．本表应在每次实施前由指导教师填写一式2份，审批后所在系（部）和指导教师各留1份。2．多名学生共用一题的，在设计内容、参数、要求等方面应有所区别。3．若填写内容较多可另纸附后。

系（部）分管领导：　　　　　教研室主任：       　　　 指导教师：     

年      月      日


目 录
第一章 绪论
1.2设计任务要求
1.3设计技术参考数据
1.4应完成的技术文件
第二章 课程设计说明书
2.1综述
2.2 被控对象稳定且不包含纯滞后环节的最少拍控制器设计
第三章 方案分析及设计
3.1 广义脉冲传递函数的求取
3.2最小拍控制器的设计
3.2.1单位阶跃信号
3.2.2单位速度信号
第四章 最小拍控制的SIMULINK仿真模型
4.1单位阶跃信号的simulink仿真模型
4.2单位速度信号的simulink仿真模型
4.3仿真模型结果分析
心得体会
参考资料



第一章 绪论
1.1引言
最小拍控制是一种直接数字设计方法。所谓最小拍控制就是要求闭环系统对于某种特定的输入在最少个采样周期内达到无静差的稳态是系统输出值尽快地跟踪期望值的变化，因此最小拍实际上是时间最优控制。
近年来，随着工业控制技术和航空航天技术的高速发展，人们对控制器的要求也越来越高。一般控制器具有以下要求：
最小拍控制是一种直接数字设计方法。所谓最小拍控制就是要求闭环系统对于某种特定的输入在最少个采样周期内达到无静差的稳态使系统输出值尽快地跟踪期望值的变化。因此最小拍控制实际上是时间最优控制。
在数字随动控制系统中，要求系统的输出值尽快地跟踪给定值的变化，最控制就是为满足这一要求的一种离散化设计方法。所谓的最小拍控制，就是要求闭环系统对于某种特定的输入在最少个采样周期内达到无静差的稳态，且闭环脉冲传递函数有以下形式：

式中，N是可能情况下的最小正整数。这一形式表明闭环系统的脉冲响应在N个采样周期后变为零，从而意味着系统在N拍之内达到稳态。但是最小拍控制器有其局限性：1、最小拍控制器对典型输入的适应性较差。一种典型的最小拍闭环脉冲传递函数 2、最小拍控制器的可实现性问题。对于某些对象的脉冲传递函数，所设计的闭环脉冲传递函数,系统的响应超前于被控对象的输入，这在实际中是实现不了的。3、最小拍控制的稳定性问题。在选择时必须有一个约束条件的零点和不稳定极点能够完全对消。
1.2设计任务要求

采用零阶保持器的单位反馈离散系统，被控对象为，如下图所示，其中为零阶保持器，为被控对象，即为待设计的最少拍控制器。设计实现最小拍控制的simulink仿真模型，要求按照单位阶跃输入和单位速度输入设计最小拍控制器，观察其输出曲线，整定参数后，系统阶跃响应超调<10%并且分析最小拍控制器设计的特点。

最少拍系统框图

1.3设计技术参考数据
1.4应完成的技术文件

第二章 课程设计说明书
2.1综述
在采样系统中，时间经过一个采样周期称为一拍。最少拍系统设计，是指系统在典型输入信号(如阶跃信号，速度信号，加速度信号等)作用下，经过最少拍(有限拍)，使系统输出的稳态误差为零。所以，最少拍控制系统的性能指标包括系统稳定、在典型输入下稳态误差为零、系统的调节时间最短或尽可能短，即最少拍系统对闭环脉冲传递函数的要求是稳定、准确和快速。本课程设计针对稳定、不含纯滞后环节的被控对象，来推导数字控制器D(z)具有的形式。

2.2 被控对象稳定且不包含纯滞后环节的最少拍控制器设计

控制系统结构如图1所示，其中H0(s)为零阶保持器，GP(s)为被控对象，D(z)即为待设计的最少拍控制器。

图1 最少拍随动系统框图

定义广义被控对象的脉冲传递函数为

广义被控对象的脉冲传递函数在z平面单位圆上及单位圆外没有极点，且不含有纯滞后环节。

闭环脉冲传递函数为        

                         (1)

误差脉冲传递函数      

                (2)

数字控制器                  

                    (3)

根据式(2)知

                                               (4)

将其展开成如下形式：

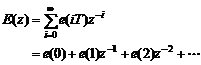              (5)

由式(6.4)可知，E(z)与系统结构Φe(z)及输入信号R(z)有关。由式(5)可以看出，根据最少拍控制器的快速性设计准则，系统输出应在有限拍N拍内和系统输入一致，即i≥N之后，e(i)=0，也就是说，E(z)只有有限项。因此，在不同输入信号R(z)作用下，根据使E(z)项数最少的原则，选择合适的Φe(z)，即可设计出最少拍无静差系统控制器。

常见的典型输入信号有：

单位阶跃输入         

单位速度输入         

单位加速度输入        

……

一般地，典型输入信号的z变换具有如下形式：

                          (6)

式中，A(z-1)是不包含(1-z-1)因式的z-1的多项式。

将式(6)代入式(4),得到

                (7)

因此，从准确性要求来看，为使系统对式(6.6)的典型输入信号无稳态误差，Φe(z)应具有的一般形式为：

                  (8)

式中，F(z-1)是不含(1-z-1)因式的z-1的有限多项式。根据最少拍控制器的设计原则，要使E(z)中关于z-1的项数最少，应该选择合适的Φe(z)，即选择合适的p及F(z-1) ，一般取F(z-1)=1，p=m。式(8)及式(3)是设计最少拍控制系统的一般公式。

在不同典型输入下，数字控制器的形式不同。

(1) 单位阶跃输入r(t)=1(t)

为使E(z)项数最少，选择p=1，F(z-1)=1，即Φe(z)=1-z-1，则

由z变换定义可知e(t)为单位脉冲函数，即

也就是说，系统经过1拍，输出就可以无静差地跟踪上输入信号,此时系统的调节时间ts=T，T为系统采样时间。

(2) 单位速度输入r(t)=t

由式(8)易知，选择p=2, F(z-1)=1, 即Φe(z)=(1-z-1)2，则：

则e(0)=0,e(T)=T,e(2T)=e(3T)=e(4T)=…=0，即系统经过2拍，输出无静差地跟踪上输入信号，系统的调节时间ts=2T。

(3) 单位加速度输入r(t)=t2/2

由式(7)可知，选择p=3，F(z-1)=1，即φe(z)=(1-z-1)3，可使E(z)有最简形式：

则e(0)=0, ，，e(3T)=e(4T)=…=0，即经过3拍，系统的输出可以无静差地跟踪上输入,即系统调节时间ts=3T。

由上面讨论可以看出，在进行最少拍控制器设计时，误差脉冲传递函数Φe(z)的选取与输入信号的形式密切相关，对于不同的输入信号r(t)，所要求的误差脉冲传递函数Φe(z)不同。所以这样设计出的控制器对各种典型输入信号的适应能力较差。若运行时的输入信号与设计时的输入信号形式不一致，将得不到期望的最佳性能。

表1 三种典型输入信号形式下的最少拍控制器设计结果


第三章 方案分析及设计

3.1 广义脉冲传递函数的求取

根据设计任务要求，设广义被控对象的传递函数为

      
由Z变换，得
带入，得
                     
                     
3.2最小拍控制器的设计
最小拍系统输入信号形式不同，数字控制器也不同，根据表1三种典型输入信号形式下的最少拍控制器设计结果，分别设计单位阶跃输入和单位速度输入相应的最小拍控制器。

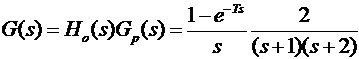
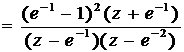
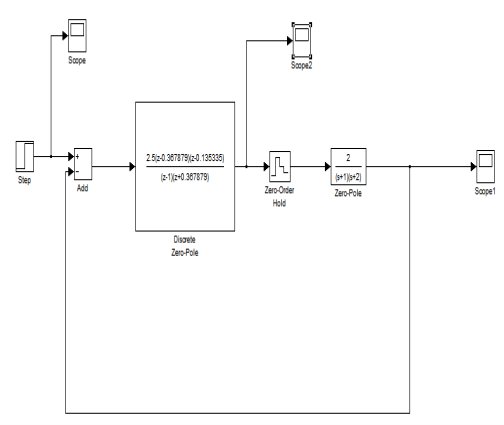
3.2.1单位阶跃信号

    当时，由Z变换得，
因此
数字控制器
         
               

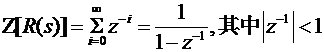
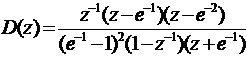
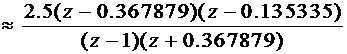
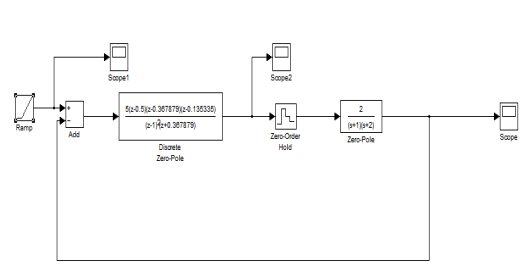
3.2.2单位速度信号

当时，由Z变换得，
设,则利用公式，得
因此
数字控制器
         
               

第四章 最小拍控制的simulink仿真模型
4.1单位阶跃信号的simulink仿真模型

4.2单位速度信号的simulink仿真模型

4.3仿真模型结果分析
当输入信号为单位阶跃信号时，按照最小拍控制策略设计的数字控制器，实现输入经过一拍后，在采样时刻系统稳态误差为零，输出跟踪输入但在采样点间，系统输出有纹波存在。
当输入信号为单位速度信号时，按照最小拍控制策略设计的数字控制器，实现输入经过两拍后，在采样时刻系统稳态误差为零，输出跟踪输入，但在采样点间，系统输出有纹波存在。
综上所述，被控对象稳定且不包含纯滞后环节，按最少拍原则设计数字控制器，虽然设计方法直观简单，又便于在计算机上实现，但也存在着缺点。
①系统输出在采样点间存在纹波，最少拍设计是保证在采样点上稳态误差为零，而在采样点之间系统输出可能存在波动，其原因在于数字控制器的输出经过两拍后不为零或为常值，而是出于振荡收敛。
②系统适应性差，最少拍原则是根据某种典型输入信号设计的，对其它输入信号不一定是最少拍，甚至可能产生很大的超调和静差。
③控制幅值的约束最少拍设计实质上是时间最优调节系统，在此过程中，对数字控制器的输出没有做任何约束，但实际上控所能提供的能量是有限，所以采用最少拍原则设计的计算机控制系统，由于被控对象存在饱和特性，系统响应输出不一定满足最少拍目的。
心得体会
这次课程设计我掌握了许多知识，不同于以往的课程设计，《计算机控制》课设的包经过一星期的《计算机控制》课程设计，收获了很多。通过这几天的学习，确实含面相当的广泛，包括对上课时的理论基础的回顾还有对数学工具MADLAB的学习掌握及单片机的使用。是一次对前面所学习科目的综合设计。 在这次课程设计中，我学到了很多设计数字控制系统的思想与方法，应用了计算机控制课程上学到的知识，还用到了自动控制原理、模拟电子技术中的相关知识，给我提供了一个将所学的课程联系在一起，并应用于实践的机会。
参考资料
[1] 张艳兵.王忠庆，鲜 浩.计算机控制技术[M].北京：国防工业出版社，2006
[2] 胡寿松.自动控制原理胡（第五版）北京：科学出版社，2007
[3] 楼顺天.基于MATLAB的系统分析与设计（第2版），2005
[4] 张养安、刘林章，MATLAB软件在数据处理中的应用， 2005

完整论文下载（word格式 可编辑）：
最小拍控制系统2.doc (185.5 KB, 下载次数: 14)


作者: admin    时间: 2017-7-25 03:25
好资料，51黑有你更精彩!!!



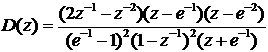
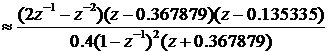
欢迎光临 (http://www.51hei.com/bbs/) Powered by Discuz! X3.1