四元数欧拉角解算,姿态解算中要用到的
- 评估一个物体在空间的姿态,一般都会想到通过该物体与参考平面的倾斜角,就是斜面与斜面之间的夹角。但是计算起来实际上我们要把这个过程分解成很多个矢量。所以解算姿态的时候可以把刚体旋转分解成三个轴上的欧拉角
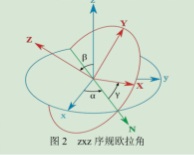 - 首先稍微说一下,欧拉角就是刚体绕三个轴的旋转角度。欧拉角与旋转角度和旋转轴的旋转顺序有关。但是标准上规定XYZ轴为旋转轴顺序。欧拉旋转与外界的参考系并没有关系。平时6050得出来的Yaw(绕Z轴)、Pitch(绕X轴)、Roll(绕Y轴)这三个是以地球作为参考系(一般以东、北、天三个方向为参考初始点),所以要区分的是欧拉角本身是以刚体本身为坐标轴的概念。
 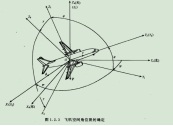 - 下面介绍一下欧拉角的致命缺点 Gimbal Lock(万向节死锁)
这个先用一句话囊括一下:不同的坐标值对应空间同一个位置,多个坐标值对应同一个位置的不一致性是造成死锁的根源。
然后就举个例子:
假如我们有一个望远镜和一个用来放望远镜的三脚架,(我们将)三脚架放在地面上,使支撑望远镜的三脚架的顶部是平行于地平面(参考平面)的,以便使得竖向的旋转轴(记为 x 轴)是完全地垂直于地平面的。现在,我们就可以将望远镜饶 x 轴旋转 360 度,从而观察(以望远镜为中心的)水平包围圈的所有方向。通常将正北朝向方位角度记为 0 度方位角。第二个坐标轴,即平行于地平面的横向的坐标轴(记为 y 轴)使得望远镜可以饶着它上下旋转,通常将地平面朝向的仰角记为 0 度,这样,望远镜可以向上仰+90 度指向天顶,或者向下-90 度指向脚底。好了,万事俱备。现在,天空中(包括地面上)的每个点只需要唯一的一对 x 和 y 度数就可以确定。比如 x=90 度,y=45 度指向的点是位于正东方向的半天空上。
现在,看看万向节死锁是怎么发生的。一次,我们探测到有一个飞行器贴地飞行,位于望远镜的正东方向(x=90 度,y=10 度),朝着我们直飞过来,我们跟踪它。飞行器飞行方向是保持 x 轴角度 90 度不变,而 y 向的角度在慢慢增大。随着飞行器的临近,y 轴角增长的越来越快且当 y 向的角度达到 90 度时(即将超越),突然它急转弯朝南飞去。这时,我们发现我们不能将望远镜朝向南方,因为此时 y 向已经是 90 度,造成我们失去跟踪目标。这就是万向节死锁!
为什么说不能将望远镜朝向南方呢,让我们看看坐标变化,从开始的(x=90 度,y=10度)到(x=90 度,y=90 度),这个过程没有问题,望远镜慢慢转动跟踪飞行器。当飞行器到达(x=90 度,y=90 度)后,坐标突然变成(x=180 度,y=90 度)(因为朝南),x 由 90突变成 180 度,所以望远镜需要饶垂直轴向 x 轴旋转 180-90=90 度以便追上飞行器,但此时,望远镜已经是平行于 x 轴,我们知道饶平行于自身的中轴线的的旋转改变不了朝向,就象拧螺丝一样,螺丝头的指向不变。所以望远镜的指向还是天顶。而后由于飞行器飞远,坐标变成(x=180 度,y<90 度)时,y 向角减小,望远镜只能又转回到正东指向,望’器’兴叹。这说明用 x,y 旋转角(又称欧拉角)来定向物体有时并不能按照你想像的那样工作,象上面的例子中从(x=90 度,y=10 度)到(x=90 度,y=90 度),按照欧拉角旋转确实可以正确地定向,但从(x=90 度,y=90 度)到(x=180 度,y=90 度),再到(x=180 度,y<90 度),按照欧拉角旋转后的定向并非正确。我的理解是坐标值的变化和飞行器空间的位置变化一一对应,但是从(x=90 度,y=90 度)到(x=180 度,y=90 度),再到(x=180 度,y<90度)这个变化,飞行器位置是连续的变化,但坐标值的变化却不是连续的(从 90 突变到180),其原因在于(x=90 度,y=90 度)和(x=180 度,y=90 度)甚至和(x=任意度,y=90 度)这些不同的坐标值对应空间同一个位置。。。
同样对于2维或者3维都是一样的(例子是抄的、、、) - 现在介绍一下方向余弦,为什么类?一方面方向余弦可以表示矢量在坐标轴中的位置,二是可以简化运算。详见下。。
刚刚说过可以用方向余弦表示矢量在坐标轴的位置,也就是说可以得出载体坐标轴xyz分别与参考坐标轴XYZ的方向余弦。形成余弦矩阵
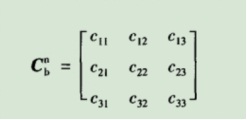
第i行、第j列的元素表示参考坐标系i轴和载体坐标系j轴夹角的余弦。
回过头来再比较一下欧拉角和方向余弦其实没有什么区别,就是用方向余弦表示欧拉角。这两个的坐标变换在《惯性导航》里面都有相应的推导。(此处略)
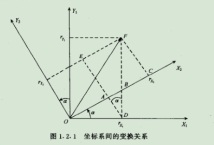
三个坐标轴的变换用矩阵表示就是这样

此处再说明一下矩阵的意义。
C 表示坐标系1到坐标系2的变换矩阵
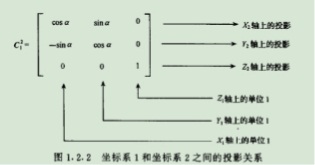
在线性代数中两复杂矩阵的变化可通过有限的矩阵相乘的运算获得,当然在坐标系中同样也适用。两坐标系任何复杂的角位置关系都可以看做有限次基本旋转的组合
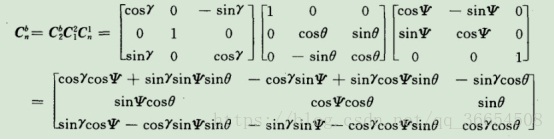
按上面推论,此矩阵的下面三个就是三轴对应的方向余弦,γ、θ、ψ就是欧拉角。 不管怎么说,要做到表示三维空间的矢量就要用到四元数。。。。原因的话就不扯了,具体可以看看百度了解一下。。。 - 四元数的表示方式:
 - 下面说一下四元数是如何表示旋转的。。。。
这个过程可以大概给一个定义:一个单位四元数可以表示一个旋转
大概意思就是:从一个坐标系转换到另一个坐标系可以通过绕一个定义在参考坐标系中的矢量u的单次转动来实现。
设 Q = a + bi + cj +dk ,我们可以写成[w,v],其中 w=a,v=bi + cj +dk。那么,v 是矢量,表示三维空间里的旋转轴。w 标量,表示旋转角度。所以,一个四元数可以表示一个完整的旋转。但要注意只有单位四元数才可以表示旋转,这个是约束条件。
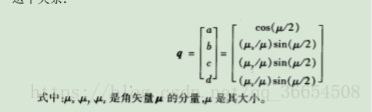 - 这个就是表示参考坐标系绕矢量u旋转w度可以转换到载体坐标系。
还有一种变法就是是旋转载体坐标系可以转换到参考坐标系。这两种都是一样的意思

其中 是绕旋转轴旋转的角度, 为旋转轴在 x,y,z 方向的分量,就是方向余弦也就确定了旋转轴 - 利用四元数进行矢量变换
 - 8、欧拉角、方向余弦、四元数的关系
先配个公式

通过上图可知四元数可以通过欧拉角或者方向余弦表示。反之,也一样。看下图。

欧拉角直接表示四元数:

方向余弦表示欧拉角:
 对补偿传感器的PID还没看懂,第一次写。。多担待
完整的Word格式文档51黑下载地址: |