傅里叶分析在电力系统中的具体应用 利用傅里叶变换对谐波进行分析 摘要:在供电系统中谐波电流的出现已经有许多年了。过去,谐波电流是由电气化铁路和工业的直流调速传动装置所用的,由交流变换为直流电的水银整流器所产生的。近年来,产生谐波的设备类型及数量均已剧增,并将继续增长。所以,必须很慎重地考虑谐波和它的不良影响,以及如何将不良影响减少到最小。本文基于傅里叶变换既可以检测谐波又可以用于频谱的分析,对电力系统的谐波进行了研究和探索。 关键词:电力系统 谐波 傅里叶变换 正文: 一、谐波及其产生原因 所谓谐波,是随周期性交流量进行傅里叶级数分解,得到的频率大于1 的整数倍分量。在理想的干净供电系统中,电流和电压都是正弦波的。这不但给电力系统的分析设计带来方便,而且使系统及用电设备的运作处于最佳状态。在只含线性元件(电阻、电感及电容)的简单电路里,流过的电流与施加的电压成正比,流过的电流是正弦波。但在实际的供电系统中,由于电力系统中某些设备和负荷的非线性特性,即所加的电压与产生的电流不成线性比例而造成的波形畸形。当电力系统向非线性设备及负荷供电时,这些设备或负荷在传递(如变压器)、变换(如交直流换流器)、吸收(如电弧炉)系统发电机所供给的基波能量的同时,又把部分基波能量转换为谐波能量,向系统倒送大量的高次谐波,使电力系统的正弦波形畸变,电能质量降低。任何周期性波形均可通过傅里叶级数分解为一个基频正弦波加上许多谐波频率的正弦波。谐波频率是基频的整倍数,例如基频为50Hz,二次谐波为100Hz,三次谐波则为150Hz。因此畸变的电流波形可能有二次谐波、三次谐波……可能直到第三十次谐波组成。 二、谐波的危害及消除谐波的必要性 电网谐波造成电网污染,正弦电压波形畸变,使电力系统的发供用电设备出现许多异常现象和故障,情况日趋严重。电力系统中谐波的危害是多方面的,概括起来有以下几个方面: 1. 对供配电线路的危害 (1) 影响线路的稳定运行:供配电系统中的电力线路与电力变压器一般采用电磁式继电器、感应式继电器或晶体管继电器予以检测保护,使得在故障情况下保证线路与设备的安全。但由于电磁式继电器与感应式继电器对10%以下含量高达40%时又导致继电保护误动作,因而在谐波影响下不能全面有效地起到保护作用。晶体管继电器虽然具有许多优点,但由于采用了整流取样电路,容易受谐波影响,产生误动或拒动。这样,谐波将严重威胁供配电系统的稳定与安全运行。 (2) 影响电网的质量:电力系统中的谐波能使电网的电压与电流波形发生畸变。如民用配电系统中的中性线,由于荧光灯、调光灯、计算机等负载,会产生大量的奇次谐波,其中3次谐波的含量较多,可达40%;三相配电线路中,相线上的3的整数倍谐波在中性线上会叠加,使中性线的电流值可能超过相线上的电流。另外,相同频率的谐波电压与谐波电流要产生同次谐波的有功功率与无功功率,从而降低电网电压,浪费电网的容量。 2. 对电力设备的危害 (1)对电力电容器的危害:当电网存在谐波时,投入电容器后其端电压增大,通过电容器的电流增加得更大,使电容器损耗功率增加。对于膜纸复合介质电容器,虽然允许有谐波时的损耗功率为无谐波时损耗功率的1.38倍;对于全膜电容器允许有谐波时的损耗功率为无谐波时的1.43倍,但如果谐波含量较高,超出电容器允许条件,就会使电容器过电流和过负荷,损耗功率超过上述值,使电容器异常发热,在电场和温度的作用下绝缘介质会加速老化。尤其是电容器投入在电压已经畸变的电网中时,还可能使电网的谐波加剧,即产生谐波扩大现象。另外,谐波的存在往往使电压呈现尖顶波形,尖顶电压波易在介质中诱发局部放电,且由于电压变化率大,局部放电强度大,对绝缘介质更能起到加速老化的作用,从而缩短电容器的使用寿命。一般来说,电压每升高10%,电容器的寿命就要缩短1/2左右。再者,在谐波严重的情况下,还会使电容器鼓肚、击穿或爆炸。 (2)对电力变压器的危害:谐波使变压器的铜耗增大,其中包括电阻损耗、导体中的涡流损耗与导体外部因漏磁通引起的杂散损耗都要增加。谐波还使变压器的铁耗增大,这主要表现在铁心中的磁滞损耗增加,谐波使电压的波形变得越差,则磁滞损耗越大。同时由于以上两方面的损耗增加,因此要减少变压器的实际使用容量,或者说在选择变压器额定容量时需要考虑留出电网中的谐波含量。除此之外,谐波还导致变压器噪声增大,变压器的振动噪声主要是由于铁心的磁致伸缩引起的,随着谐波次数的增加,振动频率在1KHZ左右的成分使混杂噪声增加,有时还发出金属声。 (3)对电力电缆的危害:由于谐波次数高频率上升,再加之电缆导体截面积越大趋肤效应越明显,从而导致导体的交流电阻增大,使得电缆的允许通过电流减小。另外,电缆的电阻、系统母线侧及线路感抗与系统串联,提高功率因数用的电容器及线路的容抗与系统并联,在一定数值的电感与电容下可能发生谐振。 (4)对用电设备的危害 ①对电动机的危害:谐波对异步电动机的影响,主要是增加电动机的附加损耗,降低效率,严重时使电动机过热。尤其是负序谐波在电动机中产生负序旋转磁场,形成与电动机旋转方向相反的转矩,起制动作用,从而减少电动机的出力。另外电动机中的谐波电流,当频率接近某零件的固有频率时还会使电动机产生机械振动,发出很大的噪声。 ②对低压开关设备的危害:对于配电用断路器来说,全电磁型的断路器易受谐波电流的影响使铁耗增大而发热,同时由于对电磁铁的影响与涡流影响使脱扣困难,且谐波次数越高影响越大;热磁型的断路器,由于导体的集肤次应与铁耗增加而引起发热,使得额定电流降低与脱扣电流降低;电子型的断路器,谐波也要使其额定电流降低,尤其是检测峰值的电子断路器,额定电流降低得更多。由此可知,上述三种配电断路器都可能因谐波产生误动作。对于漏电断路器来说,由于谐波汇漏电流的作用,可能使断路器异常发热,出现误动作或不动作。对于电磁接角器来说,谐波电流使磁体部件温升增大,影响接点,线圈温度升高使额定电流降低。对于热继电器来说,因受谐波电流的影响也要使额定电流降低。在工作中它们都有可能造成误动作。 (5)对弱电系统设备的干扰:对于计算机网络、通信、有线电视、报警与楼宇自动化等弱电设备,电力系统中的谐波通过电磁感应、静电感应与传导方式耦合到这些系统中,产生干扰。其中电感应与静电感应的耦合强度与干扰频率成正比,传导则通过公共接地耦合,有大量不平衡电流流入接地极,从而干扰弱电系统。 (6)影响电力测量的准确性:目前采用的电力测量仪表中有磁电型和感应型,它们受谐波的影响较大。特别是电能表(多采用感应型),当谐波较大时将产生计量混乱,测量不准确。 (7)谐波对人体有影响:从人体生理学来说,人体细胞在受到刺激兴奋时,会在细胞膜静息电位基础上发生快速电波动或可逆翻转,其频率如果与谐波频率相接近,电网谐波的电磁辐射就会直接影响人的脑磁场与心磁场。 因此我们必须对电力系统中的谐波成分进行精确适时的分析和检测。 传统的谐波分析的理论基 础是傅里叶分析,随着计算机、微处理器的广泛应用,数字技术在这一领域越来越多的被采用,出现了离散采样的傅里叶变换(又称为快速傅里叶变换FFT),电力系统的谐波分析目前大多是通过该方法实现的。离散傅里叶变换所要处理的是经过采样和A/D转换得到的数字信号,但由于傅里叶变换对无限长的信号做了截断,因而造成了变换的泄露现象,产生误差。此外,对于离散傅里叶变换来说,如果不是整周期采样,那么即使信号只含有单一频率、离散傅里叶变换也不可能求出信号的准确参数,出现栅栏效应。 傅里叶变换它把一个信号函数分解为众多的频率成分,这频率又可以重构原来的信号函数,这种变换是可逆的且保持能量不变。对于满足狄里赫利条件的周期函数f(t),其周期为T,角频率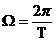 ,其傅里叶级数三角表达式为 ,其傅里叶级数三角表达式为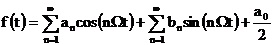 ,系数 ,系数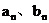 称为傅里叶系数。其中 称为傅里叶系数。其中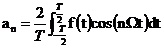 , ,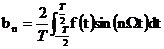 ,n=0、1、2、…。将上式中同频率项合并,可写成 ,n=0、1、2、…。将上式中同频率项合并,可写成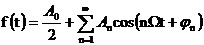 ,其中 ,其中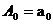 , ,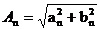 ,n=1、2、3、…, ,n=1、2、3、…,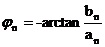 。式中表明,任何满足狄里赫利条件的周期函数可分解为直流和许多余弦(或正弦)分量。其中第一项 。式中表明,任何满足狄里赫利条件的周期函数可分解为直流和许多余弦(或正弦)分量。其中第一项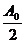 是常数项,它是周期信号中所包含的直流分量,式中第二项 是常数项,它是周期信号中所包含的直流分量,式中第二项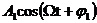 称为基波或一次谐波,它的角频率与原周期信号相同, 称为基波或一次谐波,它的角频率与原周期信号相同,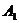 是基波振幅, 是基波振幅,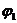 是基波初相角;式中第三项 是基波初相角;式中第三项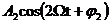 称为二次谐波,它的频率是基波频率的二倍, 称为二次谐波,它的频率是基波频率的二倍,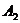 是二次谐波振幅, 是二次谐波振幅,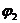 是其初相角。以此类推,还有三次、四次、…谐波。一般而言, 是其初相角。以此类推,还有三次、四次、…谐波。一般而言,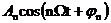 称为n次谐波, 称为n次谐波,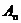 是n次谐波的振幅, 是n次谐波的振幅,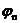 是其初相角。因此,我们将周期信号分解为各次谐波分量,从物理意义上来讲,傅里叶变换的本质就是把f(t)这个波形分解成许多不同频率的余弦波的叠加和。 是其初相角。因此,我们将周期信号分解为各次谐波分量,从物理意义上来讲,傅里叶变换的本质就是把f(t)这个波形分解成许多不同频率的余弦波的叠加和。 对于傅里叶变换目前存在问题是由于其时域和频域的局部化矛盾,难以获得信号的局部特性,且只适用于确定性的平稳信号,即使改进后的加窗傅里叶变换也仍然没有从根本上解决这一固有矛盾。所谓加窗傅里叶变换又被称为短时傅里叶变换,就是加了窗的函数的傅里叶变换(WFFT)。然而这种方法应用时,为了提高谐波计算的精度,必须要延长数据采样的长度来一直谐波间的相互干扰,一般截取长度达到10个额定工频信号周期之多。数据长度的增加,势必造成检测的延时,处理数据的增多,将加重系统的计算负担,这些都对电力系统的实时检测造成了影响。 四、窗函数 基本定义:为了减少频谱能量泄漏,可采用不同的截取函数对信号进行截断,截断函数称为窗函数,简称为窗。 窗的引入:数字信号处理的主要数学工具是傅里叶变换.而傅里叶变换是研究整个时间域和频率域的关系。不过,当运用计算机实现工程测试信号处理时,不可能对无限长的信号进行测量和运算,而是取其有限的时间片段进行分析。做法是从信号中截取一个时间片段,然后用截取的信号时间片段进行周期延拓处理,得到虚拟的无限长的信号,然后就可以对信号进行傅里叶变换、相关分析等数学处理。无限长的信号被截断以后,其频谱发生了畸变,原来集中在f(0)处的能量被分散到两个较宽的频带中去了(这种现象称之为频谱能量泄漏)。为了减少频谱能量泄漏,可采用不同的截取函数对信号进行截断,截断函数称为窗函数,简称为窗。 对于窗函数的选择,应考虑被分析信号的性质与处理要求。如果仅要求精确读出主瓣频率,而不考虑幅值精度,则可选用主瓣宽度比较窄而便于分辨的矩形窗,例如测量物体的自振频率等;如果分析窄带信号,且有较强的干扰噪声,则应选用旁瓣幅度小的窗函数,如汉宁窗、三角窗等;对于随时间按指数衰减的函数,可采用指数窗来提高信噪比,下面简要介绍各种窗函数的优缺点。 矩形窗属于时间变量的零次幂窗。矩形窗使用最多,习惯上不加窗就是使信号通过了矩形窗。这种窗的优点是主瓣比较集中,缺点是旁瓣较高,并有负旁瓣,导致变换中带进了高频干扰和泄漏,甚至出现负谱现象。 三角窗亦称费杰(Fejer)窗,是幂窗的一次方形式。与矩形窗比较,主瓣宽约等于矩形窗的两倍,但旁瓣小,而且无负旁瓣。 汉宁窗又称升余弦窗,汉宁窗可以看作是3个矩形时间窗的频谱之和,或者说是 3个 sinc(t)型函数之和,而括号中的两项相对于第一个谱窗向左、右各移动了 π/T,从而使旁瓣互相抵消,消去高频干扰和漏能。可以看出,汉宁窗主瓣加宽并降低,旁瓣则显著减小,从减小泄漏观点出发,汉宁窗优于矩形窗.但汉宁窗主瓣加宽,相当于分析带宽加宽,频率分辨力下降。 海明窗也是余弦窗的一种,又称改进的升余弦窗。海明窗与汉宁窗都是余弦窗,只是加权系数不同。海明窗加权的系数能使旁瓣达到更小。分析表明,海明窗的第一旁瓣衰减为一42dB.海明窗的频谱也是由3个矩形时窗的频谱合成,但其旁瓣衰减速度为20dB/(10oct),这比汉宁窗衰减速度慢。海明窗与汉宁窗都是很有用的窗函数。 高斯窗是一种指数窗。高斯窗谱无负的旁瓣,第一旁瓣衰减达一55dB。高斯富谱的主瓣较宽,故而频率分辨力低.高斯窗函数常被用来截短一些非周期信号,如指数衰减信号等。 不同的窗函数对信号频谱的影响是不一样的,这主要是因为不同的窗函数,产生泄漏的大小不一样,频率分辨能力也不一样。信号的截断产生了能量泄漏,而用FFT算法计算频谱又产生了栅栏效应,从原理上讲这两种误差都是不能消除的,但是我们可以通过选择不同的窗函数对它们的影响进行抑制。(矩形窗主瓣窄,旁瓣大,频率识别精度最高,幅值识别精度最低;布莱克曼窗主瓣宽,旁瓣小,频率识别精度最低,但幅值识别精度最高) 实际应用的窗函数,可分为以下主要类型: a) 幂窗--采用时间变量某种幂次的函数,如矩形、三角形、梯形或其它时间(t)的高次幂; b)三角函数窗--应用三角函数,即正弦或余弦函数等组合成复合函数,例如汉宁窗、海明窗等; c)指数窗--采用指数时间函数,如 形式,例如高斯窗等。 五、应用举例 已知我国电网电压有效值为220V,峰值为311V,电网电压除含有频率为50Hz的基频电压外,还含有谐波分量,设某一电压的函数形式为 y=sin(100*pi*t)+0.4*sin(300*pi*t)+sin(600*pi*t)+0.8*sin(800*pi*t); 利用MATLAB进行仿真并观察波形如下: 

图1 由图1可以看出,此电压经过傅里叶变换后,波形整体有较大的波动,基波占波形的主要部分,另一方面三、五、七次谐波对波形影响大,因为电网一般是平衡的三相系统,在平衡的三相系统中,偶次谐波互相抵消,是没有危害的,而高次谐波对波形影响较小,所以我们要做的就是尽量减小三五七次谐波的含量,在此基础上分别加窗函数进行仿真实验,如:加汉宁窗后,波形如下: 
图2 通过图2可看出虽然基波的幅度减小了但同时三次谐波的幅度也同样减小了,而且对于五次和七次谐波甚至直接消失,与上图1对比可知已达到我们所需要的要求。作为经典的信号分析方法,傅里叶变换具有正交、完备等许多优点,能准确的反映平稳谐波的频率特性,因而在信号分析领域得到广泛应用。采用傅里叶变换测量谐波,精度较高,功能较多,使用方便。其缺点是需要一定时间的电流值,且需要进行两次变换,它的计算量大,计算时间长,从而使得检测时间较长,检测结果实时性较差。而且在采样过程中,当信号频率和采样频率不一致时,使用该方法会产生频谱泄露效应和栅栏效应,使计算出的信号参数,即频率、幅值和相位,不准确,尤其是相对的相位误差很大,无法满足测量精度的要求,因此必须对算法进行改进,加快测量速度。基于快速傅里叶变换的谐波测量时当今应用最广泛的一种高效变换算法,它可以直接得到波形各频谱分量。而各种加窗的傅里叶变换算法的提出使得傅里叶变换的应用越来越广泛。
程序如下:
Fs=1100;%大于2倍最大谐波频率
T=1/Fs;
P=100;
t=(0:P-1)*T;
%% 采样个数
H=2^nextpow2(P);
%% 采样信号
y=sin(100*pi*t)+0.4*sin(300*pi*t)+sin(600*pi*t)+0.8*sin(800*pi*t);
subplot(4,2,[1,2])
plot(t,y)
title('原始信号')
xlabel('时间(t)')
ylabel('幅值')
Y=fft(y,H)/P;
f=Fs/2*linspace(0,1,H/2+1);
subplot(4,2,3)
plot(f,2*abs(Y(1:H/2+1)))
title('fft后')
xlabel('频率(Hz)')
ylabel('幅度|Fn|')
hanningc = hann(length(y));%加汉宁窗
yt2 = y.*hanningc';
Y=fft(yt2,H)/P;
f=Fs/2*linspace(0,1,H/2+1);
subplot(4,2,5)
plot(f,2*abs(Y(1:H/2+1)))
title('加汉宁窗')
xlabel('频率(Hz)')
ylabel('幅度|Fn|')
以上的Word格式文档51黑下载地址:
 张明轶.docx
(75.84 KB, 下载次数: 42)
张明轶.docx
(75.84 KB, 下载次数: 42)
|