|
累积梳状(CIC)滤波器分析与设计 1、累积梳状(CIC)滤波器的分析 所谓累积梳状滤波器,是指该滤波器的冲激响应具有如下形式: 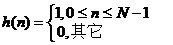 (1) (1) 式中 为梳状滤波器的系数长度(后面将会看到这里的 为梳状滤波器的系数长度(后面将会看到这里的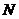 也就是抽取因子)。根据Z变换的定义,滤波器的Z变换为: 也就是抽取因子)。根据Z变换的定义,滤波器的Z变换为: 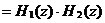 (2) (2) 式中, 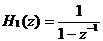 (3) (3) 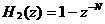 (4) (4) 其实现框图如图1所示: 可见,CIC滤波器是由两部分组成:累积器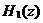 和梳状滤波器 和梳状滤波器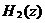 的级联,这就是为什么称之为累积梳状滤波器的原因。下面分析一下梳状滤波器的幅频特性。 的级联,这就是为什么称之为累积梳状滤波器的原因。下面分析一下梳状滤波器的幅频特性。 把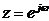 代入可得 代入可得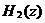 的频率响应为: 的频率响应为: 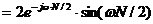 (5) (5) 其幅频特性为: 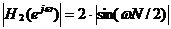 (6) (6) 若设N=7,就可以得到如图2所示的相应的频谱特性曲线: 由图2可以清楚地看到: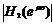 的形状犹如一把梳子,故把其形象地称之为梳状滤波器。同样可以求得累积器 的形状犹如一把梳子,故把其形象地称之为梳状滤波器。同样可以求得累积器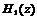 的频率响应为: 的频率响应为:  (7) (7) 故CIC滤波器的总频率响应为:  (8) (8) 式中, 为抽样函数,且 为抽样函数,且 ,所以CIC滤波器在 ,所以CIC滤波器在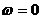 处的幅度值为 处的幅度值为 ,即: ,即:  (9) (9) CIC滤波器的幅频特性如图3所示: 在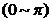 区间上称 区间上称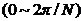 的区间为CIC滤波器的主瓣,而其它区间称为旁瓣。由图3可知,在 的区间为CIC滤波器的主瓣,而其它区间称为旁瓣。由图3可知,在 区间上随着频率的增大,旁瓣电平不断减小,其中第一旁瓣电平为: 区间上随着频率的增大,旁瓣电平不断减小,其中第一旁瓣电平为: 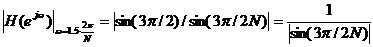 (10) (10) 比如N=7,则第一旁瓣与主瓣的电平差值为:16.9dB。不过,当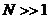 的时候,有 的时候,有 ,所以第一旁瓣电平 ,所以第一旁瓣电平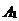 为: 为: 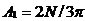 (11) (11) 因此,旁瓣与主瓣的差值 (用dB数表示)为: (用dB数表示)为: 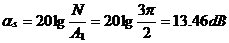 (12) (12) 可见,单级CIC滤波器的旁瓣电平是比较大的,只比主瓣低13.46dB,这也就意味着阻带衰减差,一般很难直接满足实用要求。为了减低旁瓣电平,自然会想到的方法是采用多级CIC滤波器级联的办法。设用Q级CIC级联,那么总的频率响应为: 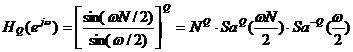 (13) (13) 同理可求得Q级CIC滤波器的旁瓣抑制为:  (14) (14) 比如当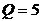 时,主瓣与旁瓣的差值为:67.3dB,这样的阻带衰减基本上能满足实际要求。但在实际的抽样率变换系统中,CIC滤波器旁瓣区域往往作为不确定 时,主瓣与旁瓣的差值为:67.3dB,这样的阻带衰减基本上能满足实际要求。但在实际的抽样率变换系统中,CIC滤波器旁瓣区域往往作为不确定 带来处理,也就是说在这些旁瓣区域不会有信号频谱(镜像或混叠频谱),因此在CIC滤波器设计中所要考虑的重要指标是抗混叠问题。这个问题放在具体的抽取率变换滤波器的分析中加以讨论。 带来处理,也就是说在这些旁瓣区域不会有信号频谱(镜像或混叠频谱),因此在CIC滤波器设计中所要考虑的重要指标是抗混叠问题。这个问题放在具体的抽取率变换滤波器的分析中加以讨论。 2、累积梳状(CIC)抽样率变换滤波器的分析 抽样率变换滤波器包括抽取滤波器和内插滤波器。根据多采样率数字信号处理理论,内插滤波器和抽取滤波器是对偶关系,也就是说抽取滤波器通过转置可以得到内插滤波器,反之亦然。因此,这里主要针对抽取滤波器展开分析,其结果也同样适用于内插滤波器。  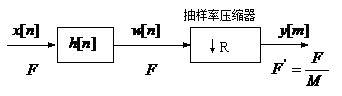 根据多采样率数字信号处理理论,抽取滤波器的结构框图如下: 根据多采样率数字信号处理理论,抽取滤波器的结构框图如下:  现若假设用N级CIC滤波器来代替 现若假设用N级CIC滤波器来代替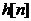 ,每一级的滤波器系数长度为R,每一级的差分延迟为M,抽取数为R,那么可以得到如图5所示的CIC抽取滤波器结构图: ,每一级的滤波器系数长度为R,每一级的差分延迟为M,抽取数为R,那么可以得到如图5所示的CIC抽取滤波器结构图:
据CIC滤波器的传递函数,图5所示的抽取滤波器结构图和图6所示的抽取滤波器结构图是等价的。  根据分支运算的换位和电路的恒等关系(具体见附录1),可以得到如图7所示的CIC抽取滤波器结构图: 根据分支运算的换位和电路的恒等关系(具体见附录1),可以得到如图7所示的CIC抽取滤波器结构图: 据图6、图7可以得到相对于高采样率 的系统函数为: 的系统函数为: 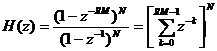 (15) (15) 从式(15)可以看到,N级CIC滤波器在功能上相当于N级完全相同的FIR滤波器的级联。如果按传统的FIR滤波器方式实现,那么N级FIR滤波器的每一级都需要RM个存储单元和一个累加器,但如果用CIC方式实现,那么N级CIC滤波器的每一级只需要M个存储单元。 CIC滤波器幅频特性具有带 带的低通特性,这可以从图3中看出来,下面具体来分析CIC抽取滤波器的幅频特性。设: 带的低通特性,这可以从图3中看出来,下面具体来分析CIC抽取滤波器的幅频特性。设:  (16) (16) 其中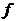 是相对于低采样率 是相对于低采样率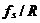 的归一化频率,把(16)式代入(15)式得到CIC滤波器的幅频特性为: 的归一化频率,把(16)式代入(15)式得到CIC滤波器的幅频特性为: 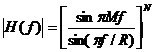 (17) (17) 如果抽取率R足够大,那么有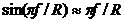 ,从而有: ,从而有:   (18) (18) 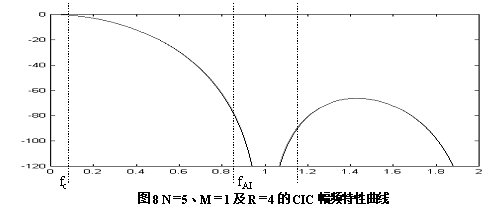 从上式可以看到,CIC的增益可达(RM)N, 差分延迟M影响着零点分布,也就是说差分延迟M可以影响幅频特性,一般M=1或2。若设N=5、M=1及R=4,那么可以得到如图8所示的幅频特性曲线: 从上式可以看到,CIC的增益可达(RM)N, 差分延迟M影响着零点分布,也就是说差分延迟M可以影响幅频特性,一般M=1或2。若设N=5、M=1及R=4,那么可以得到如图8所示的幅频特性曲线:
对于CIC抽取滤波器来说,那些零点附近的区域将会被折叠到通带而引起混叠误差,具体而言这些混叠带为:  (18) (18) 其中 ,而 ,而 1,2,┅, 1,2,┅, ,这里 ,这里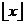 是指不大于x的最大整数。在实际设计时,混叠误差是以所有混叠带中的最大混叠误差来衡量的。如设在图8中的 是指不大于x的最大整数。在实际设计时,混叠误差是以所有混叠带中的最大混叠误差来衡量的。如设在图8中的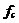 为通带截止频率,那么最大的混叠误差的位置为: 为通带截止频率,那么最大的混叠误差的位置为:  (19) (19) 而在任意频率点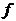 ( ( ),相对于最大值的衰减(以dB表示)为: ),相对于最大值的衰减(以dB表示)为:  (20) (20) 对于通带截止频率点的衰减,不一定需要知道 和 和 ,其实只要知道 ,其实只要知道 即可,但对于阻带截止频率点的衰减,如果只知道 即可,但对于阻带截止频率点的衰减,如果只知道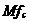 的条件是不够的,应该同时需要知道 的条件是不够的,应该同时需要知道 和 和 的值。据上述分析,就可以得到如表1所示的不同通带截止频率点的衰减值和如表2所示的不同通带截止频率下的阻带截止频率点衰减值。 的值。据上述分析,就可以得到如表1所示的不同通带截止频率点的衰减值和如表2所示的不同通带截止频率下的阻带截止频率点衰减值。 相对带宽和差分延迟乘积(  ) | 在  处的通带衰减(dB) 级数(N) | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
3、CIC抽样率变换滤波器的设计 上面已经提到过,根据多采样率数字信号处理理论,内插滤波器和抽取滤波器是对偶关系。所以不管是内插滤波器还是抽取滤波器,只要设计了一种滤波器,那么另一种滤波器也相当于得到了设计。因此,这里只研究抽取滤波器的设计问题。 根据第2部分中对抽取滤波器的分析及自己的具体设计要求,我们可以确定所要选用的CIC滤波器类型。比如:我们要求把带宽为30kHz、采样率为6MHz的信号降低为采样率为240kHz的信号,而要求通带衰减最大不得超过3dB,阻带衰减不得低于60dB。据此条件参考表1和2可知,用级数N=4、差分延迟M=1的CIC滤波器可以满足要求。但对于CIC滤波器的设计来说,那是远远不够的,这是因为CIC是数字滤波器,所以必须考虑在滤波过程中为了不产生溢出而需要的最大位数和每级可以舍去的位数。下面就来分析这两个问题。 在图7中从第j级开始到最后一级的总的系统函数为: 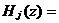  (21) (21)其中,  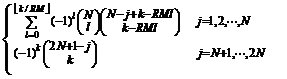 (22) (22)这组公式的获得参见附录2。 现把滤波器滤波过程中可能增加的最大值定义为最大幅度输入信号情况下最大的输出幅度。若假设信号输入位数为Bin(满刻度输入),即输入信号为2Bin,那么根据: 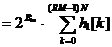 (23) (23) 故增加的值为:  (24) (24) 由(15)式和(21)式得到: 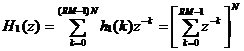 (25) (25) 因正系数的多项式乘积的展开式依然是正系数的多项式,因此有 ,这样(24)式变为: ,这样(24)式变为: 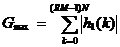 (26) (26) 另外,由(25)式,令 得到: 得到:  (27) (27) 故有: 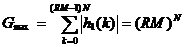 (28) (28) 从而在输入信号位数为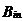 的情况下,滤波输出的最大可能位数为: 的情况下,滤波输出的最大可能位数为: 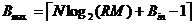 (29) (29) 这里之所以需要减1,那是因为那个符号数相乘结果中会有两位相同的符号位,所以需要去掉一位。另外,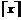 是指不小于x的最小整数。 是指不小于x的最小整数。  不仅是滤波器输出的最大可能的位数,也是每一级滤波器的最大可能位数。但在许多实际情况中, 不仅是滤波器输出的最大可能的位数,也是每一级滤波器的最大可能位数。但在许多实际情况中, 太大会使寄存器位数过宽,这是很不经济的。为了能解决这个问题,在每一级滤波器中引入四舍五入或截取的方法来减少位数。这自然需要研究一下因四舍五入或截取所引起的滤波器输出端误差,具体的方法就是通过单独研究每一级误差源(指每一级滤波器截取或四舍五入引起的误差)的均值和方差,利用统计特性研究滤波器输出端总的均值和方差。 太大会使寄存器位数过宽,这是很不经济的。为了能解决这个问题,在每一级滤波器中引入四舍五入或截取的方法来减少位数。这自然需要研究一下因四舍五入或截取所引起的滤波器输出端误差,具体的方法就是通过单独研究每一级误差源(指每一级滤波器截取或四舍五入引起的误差)的均值和方差,利用统计特性研究滤波器输出端总的均值和方差。根据实际实现时的滤波器结构(下面介绍),可以认为误差源有 个: 个: 个滤波器级因四舍五入或截取所产生的误差源和一个输出寄存器因四舍五入或截取所产生的误差源。 个滤波器级因四舍五入或截取所产生的误差源和一个输出寄存器因四舍五入或截取所产生的误差源。 一般我们认为截取比四舍五入的效果要好,但在CIC滤波器中,除了第一级和第2N+1级误差源以外,其它级误差源的输出误差统计结果不管是四舍五入还是截取都是相同的(见下面的分析)。如果在实际设计中,第一级采用全精度运算(也就是以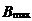 位进行运算,不截取也不舍入),那么对于设计者来讲只需要在最后一级(输出寄存器误差源)考虑采用截取还是四舍五入。 位进行运算,不截取也不舍入),那么对于设计者来讲只需要在最后一级(输出寄存器误差源)考虑采用截取还是四舍五入。 一般认为每一级误差源都是与输入信号和其它误差源不相关的白噪声,并且服从均匀概率分布。对于第j级误差源,我们可以得到误差函数为:  (30) (30) 这里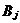 是第j级被抛掉的位数,因此可以得到第j级误差源的均值 是第j级被抛掉的位数,因此可以得到第j级误差源的均值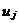 和方差 和方差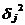 表达式: 表达式:  (31) (31)  (32) (32) 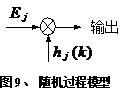 据式(21),对于第k个系数,对应的误差均值和方差为: 据式(21),对于第k个系数,对应的误差均值和方差为: 和 和 ,其随机过程模型如下图所示: ,其随机过程模型如下图所示: 因此,第j级误差源在输出端所产生的总的均值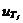 为: 为: 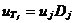 (33) (33) 其中, 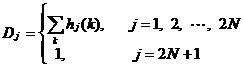 (34) (34) 同样,第j级误差源在输出端所产生的总的方差 为: 为:  (35) (35) 其中,  (36) (36) 另外,可以获证(我还未证明之): 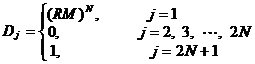 (37) (37) 从这里可以看出,对于选用截取还是舍入除了对第一级和最后一级有不同的影响外,对其它级都不会有影响。这样可以得到因截取或舍入所引起的在输出端所产生的总均值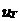 和方差 和方差 为: 为: 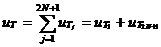 (38) (38) 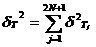 (39) (39) 现在,我们可以根据上述分析结果,在给定合适的误差限制条件下反过来确定每一级滤波器需要抛弃的位数。由于方差在所有的误差源中都受截取或舍入的影响,而均值只有对第一和最后一级产生影响,所以这里选用方差作为唯一的设计参数。 如果现在假定在输出寄存器中所保留的位数为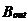 ,那么最后需要被抛弃的最低位数为: ,那么最后需要被抛弃的最低位数为:  (40) (40) 这里只所以需要加1,那是因为被抛弃的数是符号数,所以除了抛弃的数据位,还需要指定抛弃数据的符号。 为了得到前2N级滤波器中的每一级所要抛弃的位数 ,现提出以下的设计准则:前2N个误差源在输出端所产生的方差小于或等于最后一级误差源的方差,同时假定误差等同地分布在这些源中。这样就可以得到如下的不等式: ,现提出以下的设计准则:前2N个误差源在输出端所产生的方差小于或等于最后一级误差源的方差,同时假定误差等同地分布在这些源中。这样就可以得到如下的不等式: 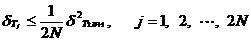 (41) (41) 而由式(30)、(32)和(35),可以得到:  (42) (42) 根据式(41)和(42)得到: 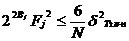 (43) (43) 以2为底求对数得到:  (44) (44) 也就是:   (45) (45) 具体的计算步骤如下: - 根据已知的R、M和N的值及式(22)求
 ; ; - 据式(36)求
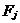 ; ; - 据式(40)、(30)、(32)和(35)式求
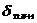 ; ; - 据(45)式求
 。 。
到此为止,我们已经讲述了CIC滤波器的选取依据和每一级位数的设计过程,下面通过一设计实例来详细介绍设计过程和实现方法。 4、设计实例及实现方法 这里讲述的例子还是要求把带宽为30kHz、采样率为6MHz的信号降低为采样率为240kHz的信号,而要求通带衰减最大不得超过3dB,阻带衰减不得低于60dB,同时要求输入和输出位数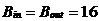 。因此,我们可以知道抽取因子R=25,而相对于低采样率的通带截止频率 。因此,我们可以知道抽取因子R=25,而相对于低采样率的通带截止频率 。根据表1和表2可以知道,N=4级和差分延迟M=1的CIC滤波器已经能够满足要求。为了简单起见,这里每一级滤波器都采用截取方式,这样我们据(29)式得到 。根据表1和表2可以知道,N=4级和差分延迟M=1的CIC滤波器已经能够满足要求。为了简单起见,这里每一级滤波器都采用截取方式,这样我们据(29)式得到 ,据(40)式得到 ,据(40)式得到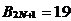 。然后根据上面的分析结果,可以从理论上推得2N滤波器级所要被抛弃的位数分别为:1,6,9,13,14,15,16和17。如果假设小数点在输出寄存器最低位的右边,这样就可以得到均值 。然后根据上面的分析结果,可以从理论上推得2N滤波器级所要被抛弃的位数分别为:1,6,9,13,14,15,16和17。如果假设小数点在输出寄存器最低位的右边,这样就可以得到均值 以及标准偏差 以及标准偏差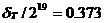 。 。 从设计的角度来看,可以说工作已经做完了,但就具体的实现而言,还需要对上述结果进行修正。比如在硬件上我们现在用4比特的基本单元来实现抽取滤波器,其具体结构如图10所示。这样为了尽量减小截尾误差但又要防止溢出,我们假定除了第一级累积级外一律使保留位数尽量靠近4的倍数,但又不达到4的倍数,具体过程如图11所示。从而得到2N滤波器级每级被抛弃的位数分别为:0,3,7,11,11,15,15和15。此时误差均值变为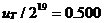 (因为 (因为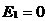 )以及标准偏差变为 )以及标准偏差变为 。 。 从而可以得到如图12所示的最终实现结构: 这里累积单元中的最低级因为没有进位,而且4bit累积单元内没有反向器,故累积单元的最后一级的进位端接低电平(即0);而对于梳状单元则不同,那时因为4bit梳状单元的内部包含有方向器,我们知道对于补码形式的数据其所对应的反向数据为各位取反并加一。比如4位补码数据0111(即7),那么其反向数据-7的补码形式为1001,显然是0111各位取反并加一。故梳状单元的最后一级进位端接高电平(即1)。 附 录 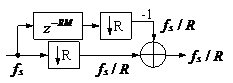 先以抽取滤波器的单级梳状级为例: 先以抽取滤波器的单级梳状级为例: 依次类推就可以得到如图7所示的抽取滤波器N级梳状级结构框图。 2、CIC抽取滤波器的系统函数推导 CIC抽取滤波器从j级开始到最后一级的系统函数包括两种情况,一种是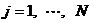 的情况,另一种是 的情况,另一种是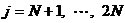 的情况。下面分别分析这两种情况下的结果。 的情况。下面分别分析这两种情况下的结果。 当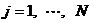 时,其系统函数为: 时,其系统函数为: 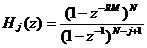 (A1) (A1) 也可以写为: 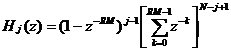 (A2) (A2) (A2)式的展开多项式中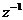 最高次幂的阶数为: 最高次幂的阶数为: 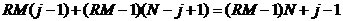 (A3) (A3) 因此,式(A1)可变为: 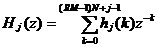 (A4) (A4) 其中 为多项式系数。另外,我们还可以把(A1)式作二项式展开得到: 为多项式系数。另外,我们还可以把(A1)式作二项式展开得到:  (A5) (A5) 如果以两多项式的交叉乘积项来表示,那么(A5)式变为: 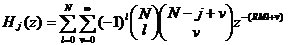 (A6) (A6) 现令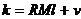 ,则可以得到 ,则可以得到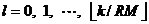 ,从而我们可以得到: ,从而我们可以得到: 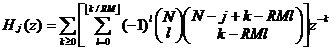 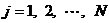 (A7) (A7)据(A4)和(A7)式可知,当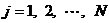 时,有: 时,有: 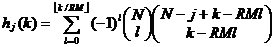 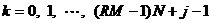 (A8) (A8)同理,当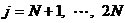 时,可以得到: 时,可以得到:  (A9) (A9)  , , 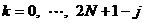 (A10) (A10) 参 考 文 献 【1】E.B.Hogenauer, “An Economical Class of Digital Filters for Decimation and Interpolation,” IEEE Trans on ASSP,VOL.ASSP-29, NO.2,April 1981. 【2】杨小牛,楼才义,徐建良著. 软件无线电原理与应用. 电子工业出版社,2001。 【3】R. E. 克劳切 L. R. 拉宾纳著,酆广增译,多采样率数字信号处理, 北京:人民邮电出版社,1988。 【4】张健,向敬成编著. 软件无线电技术导论. 电子科技大学出版社, 2001。 【5】丁玉美,高西全编著. 数字信号处理(第二版). 西安电子科技大学出版社,2001。
完整的Word格式文档51黑下载地址:
 累积梳状(CIC)滤波器分析与设计.doc
(632 KB, 下载次数: 16)
累积梳状(CIC)滤波器分析与设计.doc
(632 KB, 下载次数: 16)
|