|
锁相环的MATLAB仿真
目录
中文摘要 3
英文摘要 4
前言 6第一章 绪论7
1.1 锁相环的发展及国内外研究现状7
1.2 本文的主要内容组织9
第二章 锁相环的基本理论10
2.1锁相环的工作原理 11
2.1.1鉴相器 11
2.1.2 低通滤波器13
2.1.3 压控振荡器15
2.2锁相环的工作状态15
2.3锁相环的非线性工作性能分析 17
2.3.1跟踪性能18
2.3.2捕获性能18
2.3.3失锁状态19
2.4锁相环的稳定性20
2.5信号流程图21
2.6锁相环的优良特性21
2.7锁相环的应用22
2.7.1锁相环在调制和解调中的应用22
2.7.2锁相环在频率合成器中的应用23
2.8本章小结23
第三章锁相环的噪声分析24
3.1锁相环的输入噪声24
3.2压控振荡器的噪声24
3.3相位噪声的抑制26
3.4本章小结27
第四章 二阶锁相环仿真及结果28
4.1仿真介绍28
4.2程序代码28
4.3仿真结果34
4.4本章小结36
结 论38
致谢39
参考文献40
毕业设计小结41
摘 要 锁相环电路是使一个特殊系统跟踪另外一个系统,更确切的说是一种输出信号在频率和相位上能够与输入参考信号同步的电路,它是模拟及数模混合电路中的一个基本的而且是非常重要的模块。由于锁相环具有捕获、跟踪和窄带滤波的作用,因此被应用在通信、微处理器、以及卫星等许多领域。锁相环是通信电路里时钟电路的一个重要模块。 本文详细介绍了锁相环设计中所涉及的各项指标计。论文首先对锁相环的发展历史和研究现状做了介绍,然后从其基本工作原理出发,以传统锁相环的结构为基础,得到了锁相环的数学模型,对锁相环的跟踪性能、捕获性能、稳定性以及噪声性能等各种性能进行了分析,对锁相环的各项指标参数进行了详细推导,得出了锁相环数学分析的结论。本文详细描述了锁相环的整体电路以及鉴频鉴相器、环路滤波器、压控振荡器、分频器等电路模块。在分析和设计的同时,也采用MATLAB软件对电路进行了仿真。由于MATLAB仿真软件适合多学科、多种工作平台且功能强大、界面友好、方便快捷、语言自然并且开放性强的大型优秀应用软件,已经也已成为国内外高等院校高等数学、数值分析、数字信号处理、自动控制理论以及工程应用等课程的基本教学工具。使用Matlab对锁相环仿真的实现是方便快捷的。仿真结果表明,锁相环电路达到了设计指标要求。
前 言 锁相环(PLL)是一个能够跟踪输入信号相位的闭环自动控制系统。它在无线电技术的各个领域得到了很广泛的应用。最初,DeBellescize于1932年提出同步检波理论,首次公开发表了对锁相环路的描述,但并未引起普遍关注。直至1947年,锁相环路才第一次应用于电视接收机水平和垂直扫描的同步。从此,锁相环路开始得到了应用。由于技术上的复杂性以及较高的成本,应用锁相环路的领域主要集中于航天方面,包括轨道卫星的测速定规和深空探测等。性能要求较高的精密测量仪器和通信设备有时也用到它。到70年代,随着集成电路技术的发展,逐渐出现了集成的环路部件、通用单片集成锁相环路以及多种专用集成锁相环路,锁相环逐渐变成了一个成本低、使用简单的多功能组件,这就为锁相技术在更广阔的领域应用提供了条件。随着数字技术的发展,相应出现了各种数字锁相环,它们在数字信号传输的载波同步、位同步、相干解调等方面发挥了重要的作用。 在锁相环的开发、设计研究领域,目前已经探索出多种途径。Lindsey和Chie 讲述了到1981年他们在该领域出色完成的理论研究和实验工作。不过,大量的研究都致力于通过不同的方式实现环路鉴相器的机械化,而对于环路滤波器的设计研究则较少。典型的设计方法只是简单地实现了在模拟锁相环中应用广泛的离散式环路滤波器。这种方法存在缺陷,因为在设计过程中没有考虑到在任何采样数据系统中都固有的计算延迟。这些延迟会使环路带宽比根据连续时间方程计算出的结果更宽,指定带宽和动态下的稳态相位误差也会更大,进而降低整个环路的稳定性。 长久以来,锁相环一直是相位相干通信系统的基石。模拟锁相环一直占据着统治地位。随着微电子学领域的快速发展,具备巨大优势的数字化系统开始取代相应的模拟系统。目前的趋势是用数字化方式设计和实现锁相环。 第一章 绪 论 1.1 锁相环的发展及国内外研究现状 锁相环(PLL-Phase Locked L00P)是自动频率控制和自动相位控制技术的融合。人们对锁相环的最早研究始于20世纪30年代,其在数学理论方面的原理,30年代无线电技术发展的初期就己出现。1930年建立了同步控制理论的基础,1932年法国工程师贝尔赛什(Bellescize)发表了锁相环路的数学描述和同步检波论,第一次公开发表了对锁相环路的数学描述【1】。锁相技术首先被用在同步接收中,为同步检波提供一个与输入信号载波同频的本地参考信号,同步检波能够在低信噪比条件下工作,且没有大信号检波时导致失真的缺点,因而受到人们的关注,但由于电路构成复杂以及成本高等原因,当时没有获得广泛应用。 到了1943年锁相环路第一次应用于黑白电视接收机水平同步电路中,它可以抑制外部噪声对同步信号的干扰,从而避免了由于噪声干扰引起的扫描随机触发使画面抖动的象,使荧光屏上的电视图像稳定清。随后,在彩色电视接收机中锁相电路用来同步彩色脉冲串。从此,锁相环路开始得到了应用,迅速发展。 五十年代,随着空间技术的发展,由杰费(Jaffe)和里希廷(Rechtin)研制成功利用锁相环路作为导弹信标的跟踪滤波器,他们第一次发表了含有噪声效应的锁相环路线性理论析文章,并解决了锁相环路最佳设计化问题【2】。空间技术的发展促进了人们对锁相环路及其理论的进一步探讨,极大地推动了锁相技术的发展。 六十年代初,维特比(Viterbi)研究了无噪声锁相环路的非线性理论问题, 发表了相干通信原理的论文。最初的锁相环都是利用分立元件搭建的,由于技术和成本方面的原因,所以当时只是用于航天、航空等军事和精密测量等领域。集成电路技术出现后,直到1965年左右,随着半导体技术的发展,第一块锁相环芯片出现之后【3】,锁相环才作为一个低成本的多功能组件开始大量应用各种领域。最初的锁相环是纯模拟的(APLL),所有的模块都由模拟电路组成,它大多由四象限模拟乘法器来构建环路中的鉴相器,环路滤波器为低通滤波器(由电阻R电容C组成),压控振荡器的结构多种多样。由于APLL在稳定工作时,各模块都可以认为是线性工作的,所以也称为线性锁相环LPLL(Linear Phase.hckedbop)。APLL对正弦特性信号的相位跟踪非常好,它的环路特性主要由鉴相器的特性决定。其主要用于对信号的调制。 70年代,林特赛(Undsy)和查理斯(Chanes)在做了大量实验的基础上进行了有噪声的一阶、二阶及高阶PLL的非线性理论分析。随着人们对锁相技术的理论和应用进行的深入广泛的研究,伴随着数字电路的发展,鉴相器部分开始由数字电路代替,其它部分仍为模拟电路,这种锁相环就是最初的数字锁相环(DPLL),准确的名称为数模混合锁相环(Mixed-single PLL)。随着数模混合锁相环技术和理的不断发展和完善,其成为了锁相环的主流。 现在随着通信行中对低成本、低功耗、大带宽、高数据传输速率的需求, 集成电路不断朝着高集成度、低功耗的方向发展【4】。低功耗、高工作频率、低电压的锁相环设计中,主要的挑战是设计合适的压控振荡器和高频率的分频器,针对这方面的研究,设计师们不断提出不同的技术,如压控振荡器和分频器由原来的串接改为堆叠结构、DH-PLL结构等,随着设计人员的不断努力,锁相坏的性能不断提高,现在已经有工作频率达50GHz的锁相环,同时也在通信和航空航天等领域中发挥着越来越重要的作要。 国外自第一个锁相环集成产品问世以来,几十年问发展极为迅速,产品种类繁多,工艺日新月异。目前,除某些特殊用途的锁相环路外,几乎全部集成了,已生产出数百个品种。现在,锁相技术己经成为一门系统的理论科学,它在通信、雷达、航天、精密测量、计算机、红外、激光、原子能、立体声、马达控制以及图像等技术部门获得了广泛的应用。 美国国家半导体(Nation Semi Conductor)于2003年6月宣布推出的LMx243x系列锁相环芯片,其操作频率高达3GHz以上,适用于无线局域网、5.8GHz室内无绳电话、移动电话及基站等应用方案。低功耗、超低的相位噪声(正常化相位噪音可达到—219dBcmz)使其突显优势。 国内的浩凯微电子(上海)有限公司于2007年底研发出具有完全自主知识产权的高性能时钟锁相环IP系列产品,目前该系列产品已经过MPW硅验证。该锁相环系列采用全新的结构,独特的电荷泵和差分VCO的设计,可以抑制电源和衬底噪声对VCO的影响以确保PLL有非常低的噪声,差分VCO的独特设计可以输出时钟维持50%占空比且与VCO同频,由于不需要倍频振荡,VCO本身的功耗可降为常规设计的四分之一,有效降低了功耗。相比国外而言,我国国内的IC设计水平相对比较落后,模拟设计环节更是薄弱,PLL的技术几乎被国外垄断,国内很少有企业掌握高性能PLL核心技术, 产品更是少。CPPLL作为应用最广泛的一种锁相环,虽然它的理论己经比较成熟,但是它的设计与实现涉及到信号与系统、集成电子学、版图、半导体工艺和测试等方面,难度比较大。 1.2 本文的主要内容组织 第一章对锁相环的发展和国内外研究现状进行了介绍,说明了本课题研究的 重要意义。 第二章介绍了锁相环的基本原理,介绍了锁相环的基本构成、数学模型、工作状态及、信号流程应用及信号流程。 第三章分析了了锁相环噪声的产生原因,并在数学模型上作了说明,并给出了设计建议。 第四章是二阶环仿真源程序代码及仿真结果。 第二章 锁相环的基本理论 锁相环作为一个系统,主要包含三个基本模块:鉴相器(Phase Detector:PD)、低通滤波器(LowPass Filter:LPF),亦即环路滤波器(L00P Filter:LF),和压控振荡器(Voltage Controlled Oscillator:VCO)。这三个基本模块组成的锁相环为基本锁相环,亦即线形锁相环(LPLL),如图2.1所示。 
图2.1锁相环原理图 当锁相环开始工作时,输入参考信号的频率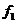 与压控振荡器的固有振荡频率 与压控振荡器的固有振荡频率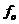 总是不相同的,即 总是不相同的,即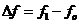 ,这一固有频率差 ,这一固有频率差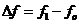 必然引起它们之间的相位差不断变化,并不断跨越 必然引起它们之间的相位差不断变化,并不断跨越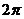 角。由于鉴相器特性是以相位差 角。由于鉴相器特性是以相位差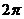 为周期的,因此鉴相器输出的误差电压总是在某一范围内摆动。这个误差电压通过环路滤波器变成控制电压加到压控振荡器上,使压控振荡器的频率 为周期的,因此鉴相器输出的误差电压总是在某一范围内摆动。这个误差电压通过环路滤波器变成控制电压加到压控振荡器上,使压控振荡器的频率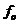 趋向于参考信号的频率 趋向于参考信号的频率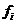 ,直到压控振荡器的频率变化到与输入参考信号的频率相等,并满足一定条件,环路就在这个频率上稳定下来。两个频率之间的相位差不随时间变化而是一个恒定的常数,这时环路就进入“锁定”状态。 ,直到压控振荡器的频率变化到与输入参考信号的频率相等,并满足一定条件,环路就在这个频率上稳定下来。两个频率之间的相位差不随时间变化而是一个恒定的常数,这时环路就进入“锁定”状态。 当环路已处于锁定状态时,如果输入参考信号的频率和相位发生变化,通过环路的控制作用,压控振荡器的频率和相位能不断跟踪输入参考信号频率的变化而变化,使环路重新进入锁定状态,这种动态过程称为环路的“跟踪”过程。而环路不处于锁定和跟踪状态,这个动态过程称为“失锁”过程。 从上述分析可知,鉴相器有两个主要功能:一个是频率牵引,另一个是相位锁定。实际中使用的锁相环系统还包括放大器、分频器、混频器等模块,但是这些附加的模块不会影响锁相环的基本工作原理,可以忽略。 2.1 锁相环的工作原理 锁相环作为一个系统,主要包含三个基本模块:鉴相器【4】、低通滤波器,亦即环路滤波器,和压控振荡器。在本节首先分析鉴相器、环路滤波器和压控振荡器. 2.1.1 鉴相器 锁相环中的鉴相器(PD)通常由模拟乘法器组成,利用模拟乘法器组成的鉴相器电路如图示:  图2.2 模拟鉴相器电路 鉴相器的工作原理是:设外界输入的信号电压和压控振荡器输出的信号电压分别为: 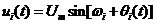 (2.1) (2.1)
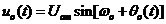 (2.2) (2.2) 式中的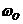 为压控振荡器在输入控制电压为零或为直流电压时的振荡角频率,称为电路的固有振荡角频率。则模拟乘法器的输出电压 为压控振荡器在输入控制电压为零或为直流电压时的振荡角频率,称为电路的固有振荡角频率。则模拟乘法器的输出电压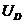 为: 为: 
(2.3) 鉴相器的传输特性为: 
图2.3 鉴相器的传输特性 鉴相器有两个主要功能:一个是频率牵引,另一个是相位锁定。实际中使用的锁相环系统还包括放大器、分频器、混频器等模块,但是这些附的模块不会影响锁相环的基本工作原理,可以忽略。 鉴相器的电路种类很多,大致可以分为四种常用类型: 1.乘法鉴相器。一般应用在模拟锁相环(LPLL)中,即线性锁相环,鉴相的范围是[+90°,-90°]; 2.异或门鉴相器。较多应用于数字锁相环中,鉴相范围同为[+90°,-90°]中,要考虑鉴相器输入的两个信号是对称的还是非对称的,如是非对称还要考虑其对PLL增益及锁相宽度的影响; 3.JK触发器型鉴相器。这种鉴相器由边沿触发,利用边沿间的间隔进行鉴相,相位误差为[+180°,-l80°]; 4.鉴频鉴相器(phase—frequency detector)。其优势就在于失锁时,它的角频率容易描述。这种角频率的描述就可以实现鉴频的功能。鉴相范围为[+360°,-360°]。 2.1.2低通滤波器 低通滤波器(LF)的将上式2.3中的和频分量滤掉,剩下的差频分量作为压控振荡器的输入控制电压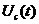 。即为: 。即为: 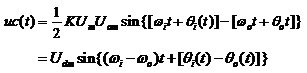 (2.4) (2.4) 式中的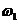 为输入信号的瞬时振荡角频率, 为输入信号的瞬时振荡角频率,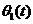 和 和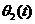 分别为输入信号和输出信号的瞬时位相,根据相量的关系可得瞬时频率和瞬时位相的关系为: 分别为输入信号和输出信号的瞬时位相,根据相量的关系可得瞬时频率和瞬时位相的关系为: 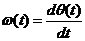
即 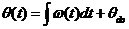 (2.5) 则,瞬时相位差 (2.5) 则,瞬时相位差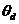 为 为 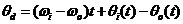 (2.6) (2.6)
对两边求微分,可得频差的关系式为: 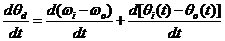 (2.7) (2.7)
上式2.7等于零,说明锁相环进入相位锁定的状态,此时输出和输入信号的频率和相位保持恒定不变的状态, 为恒定值。当上式不等于零时,说明锁相环的相位还未锁定,输入信号和输出信号的频率不等, 为恒定值。当上式不等于零时,说明锁相环的相位还未锁定,输入信号和输出信号的频率不等,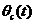 随时间而变。其数学模型为: 随时间而变。其数学模型为: 
图2.4 环路滤波器模型 环路滤波器的分类: 1.RC积分滤波器。这是结构最简单的低通滤波器,它具有低通特性,且相位滞后。当频率很高的时候,幅度趋于零,相位滞后接近于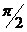 ; ; 2.无源比例积分滤波器; 3.有源比例积分滤波器。它由运算放大器组成,高增益的有源比例积分滤波器又称为理想积分滤波器。 2.1.3压控振荡器 压控振荡器(VCO)【6】的压控特性如图2.5所示: 
2.5压控振荡器特性 该特性说明压控振荡器的振荡频率 以为中心,随输入信号电压 以为中心,随输入信号电压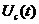 线性地变化,变化的关系如下: 线性地变化,变化的关系如下: 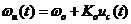 (2.8) (2.8) 上式说明当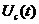 随时间而变时,压控振荡器(VCO)的振荡频率 随时间而变时,压控振荡器(VCO)的振荡频率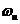 也随时间而变,锁相环进入“频率牵引”,自动跟踪捕捉输入信号的频率,使锁相环进入锁定的状态,并保持 也随时间而变,锁相环进入“频率牵引”,自动跟踪捕捉输入信号的频率,使锁相环进入锁定的状态,并保持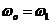 的状态不变。 的状态不变。 2.2锁相环的工作状态 锁相环有四种工作状态,即锁定状态、失锁状态、捕获过程和跟踪过程【7】。 1.锁定状态:整个环路己经达到输入信号相位的稳定状态。它指输出信号相位等于输入信号相位或者是两者存在一个固定的相位差,但频率相等。在锁定状态时,压控振荡器的电压控制信号接近平缓。 2.失锁状态:环路的反馈信号与锁相环输入信号的频率之差不能为零的稳状态。当环路的结构设计有问题,或者是输入信号超出了锁相环的应用范围的时候都会进入失锁状态。这个状态意味着坏路没有正常工作。 3.捕获过程:指环路由失锁状态进入锁定状态的过程。这个状态表明环路已经开始进入正常工作,但是还没有达到锁定的稳态。此过程应该是一个频率和相位误差不断减小的过程。 4.跟踪过程:是指在PLL环路处于锁定状态时,若此时输入信号频率或相位因其它原因发生变化,环路能通过自动调节,来维持锁定状态的过程。由于输入信号频率或者相位的变化引起的相位误差一般都不大,环路可视作线性系统。PLL的这四种状态中,前两个状态称为静态,后两个状态称为动态【8】。优秀的设计可以使PLL在上电后立刻进入捕获状态,从而快速锁定。 一般用四个参数指标来描述PLL的系统频带性能: 1.同步带:它指的是环路能保持静态锁定状态的频率范围。当环路锁定时,逐步增大输入频率,环路最终都能保持锁定的最大输入固有频差。 2.失锁带:锁相环路稳定工作时的动态极限。也就是说PLL在稳定工作状态时,输入信号的跳变要小于这个参数,PLL才能快速锁定。若输入信号的跳变大于该参数而小于捕获带,则环路还是能锁定,但是需要较长的时间。 3.捕获带:只要反馈信号和输入信号的频差在这一范围内,环路总会通过捕获而再次锁定,随着捕获过程的进行,反馈信号的频率向着输入信号频率方向靠近,经过一段时间后,环路进入快捕带过程,最终达到锁定。 4.快捕带:在此频差范围内,环路不需要经历周期跳跃就可达到锁定,实现捕获过程。  2.6锁相环不同带宽捕获示意图【5】 2.6锁相环不同带宽捕获示意图【5】
当相关频率变化比较小时,相位误差e大小将与频率的变换量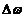 成比例。而如果频率偏移 成比例。而如果频率偏移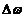 达到某一特定值时,稍有变换PLL将失去捕获相位的能力,最终失锁。这一特定值就称作PLL的同步带。这个频率范围也称作PLL稳定的静态极限范围。在失锁时,相位误差 达到某一特定值时,稍有变换PLL将失去捕获相位的能力,最终失锁。这一特定值就称作PLL的同步带。这个频率范围也称作PLL稳定的静态极限范围。在失锁时,相位误差 将无限增加下去,同步带内,信号的捕获时间也是最长的。捕获的稳定性也较差。 将无限增加下去,同步带内,信号的捕获时间也是最长的。捕获的稳定性也较差。 频率阶跃信号作为输入信号进入PLL时(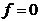 时刻频率阶跃的大小是 时刻频率阶跃的大小是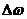 ),如果此阶跃信号引起PLL的失锁,那么就称这个频率阶跃值为锁出频率值,这个范围叫做锁相环出锁频率。这个阶跃信号频差值小于PLL的同步带。在这里,同步带可以看作是频率缓慢变化到此范围使锁相环失锁的极值;而出锁频率是突然变化到此阶跃值而引起PLL失锁。而且出锁范围也可以理解为PLL稳定的动态范围,在频率阶跃信号的跳变不超过出锁范围时PLL是满足稳定条件的。 ),如果此阶跃信号引起PLL的失锁,那么就称这个频率阶跃值为锁出频率值,这个范围叫做锁相环出锁频率。这个阶跃信号频差值小于PLL的同步带。在这里,同步带可以看作是频率缓慢变化到此范围使锁相环失锁的极值;而出锁频率是突然变化到此阶跃值而引起PLL失锁。而且出锁范围也可以理解为PLL稳定的动态范围,在频率阶跃信号的跳变不超过出锁范围时PLL是满足稳定条件的。 如果有一频差值使得平均相位误差的斜率变小,且VCO输出的频率值会越来越接近输入信号的频率,最终环路系统将重新锁定,这一关键值称作入锁频率。 假如输入信号频率与输出信号频率的偏移量 低于捕获带,则PLL将要锁定。这个过程称作快捕过程,它快于入锁过程,而这个捕获范围也小于入锁范围。 低于捕获带,则PLL将要锁定。这个过程称作快捕过程,它快于入锁过程,而这个捕获范围也小于入锁范围。 PLL捕获的过程包含频率捕获与相位捕获两个过程,通常频率捕获过程所需要的时间称为频率捕获时间(或频率牵引时间);相位捕获过程所需要的时间称为快捕时间(或相位捕获时间)。一般频率捕获时间总是大于相位捕获时间的,所以常说的捕获时间就是指频率捕获时间,不考虑相位捕获时间的影响。 2.3锁相环的非线性工作性能分析 当锁相环的相位误差大于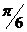 时,正弦鉴相器将不再能够线性化,环路成为非线性系统,其非线性性能表现为以下三种情况:已处于锁定状态的锁相环,当输入信号频率或压控振荡器自由振荡频率变化过大或变化速度过快时,使环路相位误差增大到鉴相器的非线性区,这种非线性环路的性能为非线性跟踪性能【9】;从接通到锁定的捕获过程中,相位误差的变化范围是很大的,环路处于非线性状 时,正弦鉴相器将不再能够线性化,环路成为非线性系统,其非线性性能表现为以下三种情况:已处于锁定状态的锁相环,当输入信号频率或压控振荡器自由振荡频率变化过大或变化速度过快时,使环路相位误差增大到鉴相器的非线性区,这种非线性环路的性能为非线性跟踪性能【9】;从接通到锁定的捕获过程中,相位误差的变化范围是很大的,环路处于非线性状 态;失锁状态时环路的频率牵引现象。 2.3.1跟踪性能 环路非线性跟踪性能指标包括稳态相位误差见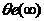 、同步带 、同步带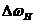 和最大同步扫描速 和最大同步扫描速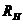 ,在这里从环路动态方程对其进行分析。输入固定频率信号的条件下,锁相环路的动态方程可变为: ,在这里从环路动态方程对其进行分析。输入固定频率信号的条件下,锁相环路的动态方程可变为: 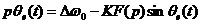 (2.9) (2.9) 环路锁定时瞬时相差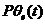 等于零,且鉴相器输出误差信号和压控振荡器控制信号均为直流,由此可得环路的稳态相位误差为: 等于零,且鉴相器输出误差信号和压控振荡器控制信号均为直流,由此可得环路的稳态相位误差为: 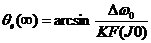 (2.10) (2.10)
上式2.10中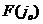 为环路滤波器的直流增益。理想二阶环的 为环路滤波器的直流增益。理想二阶环的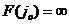 ,其稳态相位误差为: ,其稳态相位误差为: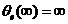 对于已经锁定的环路,缓慢增加其固有频率,环路如果还能保持锁定,则 对于已经锁定的环路,缓慢增加其固有频率,环路如果还能保持锁定,则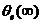 有解。使上式有解的环路固有频差的最大值就是环路的同步带,即: 有解。使上式有解的环路固有频差的最大值就是环路的同步带,即: 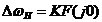 (2.11) (2.11)
则可得理想二阶环路的同步带: 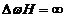 (2.12) (2.12)
上式2.12成立的前提是环路滤波器和压控振荡器都有无限大的线性工作范围,这是不符合实际的。理想二阶环的同步带是有限的,它往往受限于压控振荡器的最大控制范围。理想二阶环可以跟踪频率斜升信号,其稳态相位误差为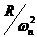 。加大频率斜升信号的斜率R,就可能使环路进入非线性跟踪状态。进一步加大R,环路就可能失锁。使环路不致失锁的尺的最大值就是最大同步扫描速率。在输入频率斜升信号的条件下有: 。加大频率斜升信号的斜率R,就可能使环路进入非线性跟踪状态。进一步加大R,环路就可能失锁。使环路不致失锁的尺的最大值就是最大同步扫描速率。在输入频率斜升信号的条件下有: 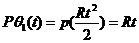 (2.13) (2.13)
把理想二阶坏的传输算子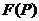 代入上式2.13可得锁定时坏路的相位误差为: 代入上式2.13可得锁定时坏路的相位误差为:  (2.14) (2.14)
当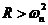 上式无解,意味着环路失锁,因此理想二阶环的最大同步扫描速率为: 上式无解,意味着环路失锁,因此理想二阶环的最大同步扫描速率为: 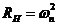 (2.15) (2.15)
2.3.2捕获性能 实际工作过程中,锁相环初始状态往往是失锁状态。环路经由失锁进入锁定状态,需要经历一个捕获过程。捕获过程分为频率捕获和相位捕获两个过程。在相位捕获中环路相位误差不会发生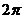 周期跳跃,捕获时间比较短,因此相位捕获也叫做快捕。与相位捕获相比,频率捕获时间较长,它构成了捕获时间的主要部分。一般而言,捕获过程中环的瞬时相差将在大范围内变化,使捕获过程表现为一种非线性现象。要想获得环路捕获性能的全部结果,需要求解环路非线性动态方程,二阶环路的动态方程是二阶非线性微分方程,在数学上是无法精确求解的,只能用近似求解的方法求解。理想二阶环的方程为: 周期跳跃,捕获时间比较短,因此相位捕获也叫做快捕。与相位捕获相比,频率捕获时间较长,它构成了捕获时间的主要部分。一般而言,捕获过程中环的瞬时相差将在大范围内变化,使捕获过程表现为一种非线性现象。要想获得环路捕获性能的全部结果,需要求解环路非线性动态方程,二阶环路的动态方程是二阶非线性微分方程,在数学上是无法精确求解的,只能用近似求解的方法求解。理想二阶环的方程为: 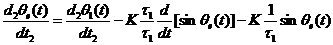 (2.16) (2.16)
设环路输入信号频率固定,则 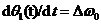 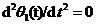 (2.17) (2.17) 代入并简化,可得理想二阶环轨迹方程:
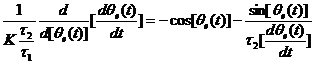 (2.18) (2.18)
由上式可得到理想二阶环的捕获特性,如下表 2.6理想二阶环的捕获特性 实际情况中环路的捕获带不会为无穷大【10】,它受到压控振荡器最大频率范围的限制。 2.3.3失锁状态 锁相环失锁时,具有频率牵引现象。当环路失锁时,环路中误差电压为上下不对称的周期性差拍信号,此差拍电压的直流分量使压控振荡器的平均频率向输入信号频率靠近,从而使环路输出信号的平均频差小于环路固有频差。 2.4锁相环的稳定性 锁相环是一个负反馈系统,要工作正常,首先必须稳定,不稳定就不能实现相位的自动调节。通常的系统稳定性,是指系统在有限输入的作用下输出有限响应。 对于线形系统而言,其稳定性与输入信号的大小无关,只取决于系统传递函数极点的位置。线形系统稳定的必要和充分条件,是系统闭环传递函数的所有点都具有负实部,或者说都位于s平面的左半部。 锁相环路本质是一个非线性系统,它的稳定性是一个非线性问题。非线性系统的稳定性取决于系统本身和输入。因此,通常把非线性系统的稳定性分为强干扰作用下和弱干扰作用下的稳定性问题,或者叫大稳定性和小稳定性问题。对于锁相环来说,前者相当于环路失锁而处于捕获状态,后者相当于同步状态。对于大稳定性问题,主要研究环路的捕捉问题。同步状态是环路的线形工作状态,所以小稳定性问题实际上是一个线形系统的稳定性问题。 判断系统稳定性的方法,通常叫巴克豪森准则【11】。对于一个反馈系统,如果其环路增益超过1,同时环路相移超过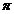 ,即同时满足起振的振幅条件和位条件,那么此反馈系统是不稳定的,巴克豪森准则判断系统稳定性的条件是: ,即同时满足起振的振幅条件和位条件,那么此反馈系统是不稳定的,巴克豪森准则判断系统稳定性的条件是:

或 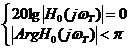 (2.19) (2.19)
公式2.19中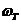 是增益临界频率,为开环增益达到0dB时的频率。 是增益临界频率,为开环增益达到0dB时的频率。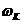 相位临界频率,为开环相移达到万时的频率。 相位临界频率,为开环相移达到万时的频率。 对于闭环不稳定的环路必有对于闭环稳定的环路,必有ωT>ωK;闭环临界的情况为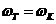 。在工程中,闭环临界的稳定情况实际是不稳定的,因为实际电路中总有引起各种参数变化的因素,产生附加相移,这些都会使一个临界稳定的坏路不稳定。所以,实际使用的环路不但是稳定的而且要远离临界条件。这就是“相位裕度”的问题,定义为丌环增益降至OdB时开环相移量与π的差值,此概念可以说明环路稳定的程度。 。在工程中,闭环临界的稳定情况实际是不稳定的,因为实际电路中总有引起各种参数变化的因素,产生附加相移,这些都会使一个临界稳定的坏路不稳定。所以,实际使用的环路不但是稳定的而且要远离临界条件。这就是“相位裕度”的问题,定义为丌环增益降至OdB时开环相移量与π的差值,此概念可以说明环路稳定的程度。 在实际的锁相环电路中,不可避免地存在一些寄生相移,它们引入了额外的高频极点,不利于环路的稳定性。环路相位裕度的理论值太小,考虑到寄生相移的影响,则实际相位裕度可能更小,会使环路不稳定。 2.5信号流程图 锁相环的原理框图如下: 
2.7锁相环原理框图 其工作过程如下: 1压控振荡器的输出Uo经过采集并分频; 2.输出和基准信号同时输入鉴相器; 3.鉴相器通过比较上述两个信号的频率差,然后输出一个直流脉冲电压Ud; 4.Ud进入到滤波器里面,滤除高频成分后得到信息Ue; 5.Ue进入到压控震荡器VCO里面,控制频率随输入电压线性地变化; 6.这样经过一个很短的时间,VCO的输出就会稳定于某一期望值。 2.6锁相环的优良特性 锁相环广泛应用于无线领域,是其自身具有较好的特性: 1.载波跟踪特性。无论输入锁相环的信号是已调制好的或未调制的,只要信号中包有载波 频率成分就可将环路设计成一个窄带跟踪滤波器,跟踪输入信号载波成分的频率与相位变化,环路输出信号就是需要提取(或复制)的载波信号。这就是环路的载波跟踪特性。 载波跟踪特性包含这三重含义:一是窄带。环路可以有效地滤除输入信号伴随的噪声和干扰。环路主要是利用环路滤波器的低通特性来实现输入信号的载频上的窄带带通特性的,这比制作普通的窄带带通滤波器容易得多。在高载频上,用锁相环路可将通带做到几赫兹那么窄,这是普通带通滤波器难以实现的。二是跟踪。环路可以在保持窄带特性的情况下跟踪输入载波频率的漂移。普通带通滤波器的频率特性是固定的,为了能接收载频漂移的输入信号,滤波器的通带带宽必须设计漂移范围,因而无法利用窄带特性来过滤噪声与干扰。三是可将弱输入载波信号放大到强信号输出。因为环路输出的是压控振荡器的信号,它是输入弱载波信号频率与相位的真实复制品,其幅度则比输入信号强的多。 2.调制跟踪特性。只要让环路有适当宽度的低频通带,压控振荡器输出信号的频率与相位就能跟踪输入调频或调相信号的频率与相位的变化,即得到输入角调制信号的复制品,这就是调制跟踪特性。利用环路的调制跟踪特性,可以制成角调制信号的调制器与解调器。 3.低门限特性。锁相环路不像一般非线性器件那样,门限取决于输入信噪比,而是由环路信噪比决定的。一般环路的通频带总比环路输入端的前置通频带窄的多,因而环路信噪比明显高于输入信噪比,环路能在低输入信噪比条件下工作,即具有低门限的优良特性。这样,只要将环路设计成窄带,就可把淹没在噪声中的微弱信号提取出来。这样的环路用于解调调频、调相信号时,可取得门限扩展的效果;用于解调数字调制信号时,可使误码率降低。 2.7锁相环的应用 2.7.1.锁相环在调制和解调中的应用 调频波的特点是频率随调制信号幅度的变化而变化。压控振荡器的振荡频率取决于输入电压的幅度。当载波信号的频率与锁相环的固有振荡频率 相等时,压控振荡器输出信号的频率将保持 相等时,压控振荡器输出信号的频率将保持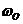 不变。若压控振荡器的输入信号除了有锁相环低通滤波器输出的信号 不变。若压控振荡器的输入信号除了有锁相环低通滤波器输出的信号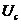 外,还有调制信号 外,还有调制信号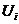 ,则压控振荡器输出信号的频率就是以 ,则压控振荡器输出信号的频率就是以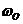 为中心,随调制信号幅度的变化而变化的调频波信号。由此可得调频电路可利用锁相环来组成,由锁相环组成的调频电路组成框图下图所示。 为中心,随调制信号幅度的变化而变化的调频波信号。由此可得调频电路可利用锁相环来组成,由锁相环组成的调频电路组成框图下图所示。 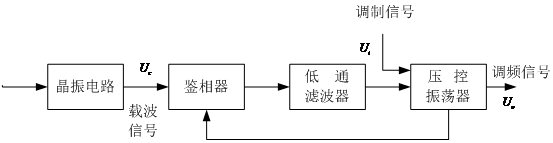 2.8锁相环组成的调频电路 2.8锁相环组成的调频电路
根据锁相环的工作原理和调频波的特点可得解调电路组成框图如图2.8所示。 2.7.2.锁相环在频率合成电路中的应用 在现代电子技术中,为了得到高精度的振荡频率,通常采用石英晶体振荡器。但石英晶体振荡器的频率不容易改变,利用锁相环、倍频、分频等频率合成技术,可以获得多频率、高稳定的振荡信号输出。输出信号频率比晶振信号频率大的称为锁相倍频器电路;输出信号频率比晶振信号频率小的称为锁相分频器电路。锁相倍频和锁相分频电路的组成框图下图所示。 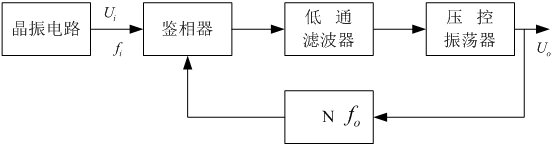 2.8锁相倍频和锁相分频电路 2.8锁相倍频和锁相分频电路
图中的N大于1时,为分频电路;当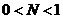 时,为倍频电路。 时,为倍频电路。 2.8本章小结 本章对锁相环系统的基本原理及组成部件进行了概括介绍,对锁相环系统的捕获、跟踪性能,动态特性以及锁相环的自身特性等一些基本性能、概念给出了相关说明,指出锁相环路所以能够得到如此广泛的应用,是由其独特的优良性能所决定的。它具有载波跟踪特性,作为一个窄带跟踪滤波器,提取淹没在噪声之中的信号,在深空测控中有着广泛的应用。 第三章锁相环的噪声分析 锁相环的输入信号和各个模块都包括了噪声源,其输出信号必然包含噪声。噪声是锁相环的重要特性,设计中必须考虑。本章节主要分析了输入信号的噪声和压控振荡器的噪声。在实际的工作过程中,压控振荡器的相位噪声是锁相环最主要的噪声。 3.1锁相环的输入噪声 如下所示,以采用RC 积分滤波器的锁相环为例。设输入和输出信号 积分滤波器的锁相环为例。设输入和输出信号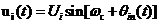 和 和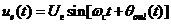 。则由前面章节可得出传输函数为: 。则由前面章节可得出传输函数为: 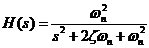 (3.1) (3.1)
如果输入相位偏差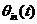 不随时间变化,即为纯正弦信号。当 不随时间变化,即为纯正弦信号。当 时, 时, 。同样,假设 。同样,假设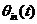 变化缓慢,则上式的分母会接近 变化缓慢,则上式的分母会接近 ,所以 ,所以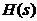 仍然等于1,这表明输出相位跟随输入相位,或者说是输出频率跟随输入频率。 仍然等于1,这表明输出相位跟随输入相位,或者说是输出频率跟随输入频率。 如果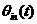 变化非常快,上式表明输出相位偏差气, 变化非常快,上式表明输出相位偏差气, 减小并最终为零,使得“ 减小并最终为零,使得“ ,即输入相位或者频率变化太快,锁相环不能跟踪输信号。输入信号的相位噪声被坏路中的低通滤波器整形最后出现在输出端。为了减小噪声,环路带宽应该尽量小,但这以降低锁定范围、限制捕获范围、降低稳定性为代价。 ,即输入相位或者频率变化太快,锁相环不能跟踪输信号。输入信号的相位噪声被坏路中的低通滤波器整形最后出现在输出端。为了减小噪声,环路带宽应该尽量小,但这以降低锁定范围、限制捕获范围、降低稳定性为代价。 3.2压控振荡器的噪声 VCO的相位噪声可以被认为是一个外加信号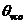 ,如下图3.1所示。在此假设, ,如下图3.1所示。在此假设,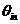 和 和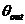 是不相关的。假设 是不相关的。假设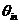 =0,即表示输入信号的相位偏差为零,输入信号为一个严格的周期信号。得到从 =0,即表示输入信号的相位偏差为零,输入信号为一个严格的周期信号。得到从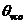 到 到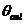 的传递函数: 的传递函数: 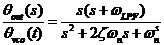 (3.2) (3.2)
由上所得的输入噪声和传递函数有相同的极点,但是它包括了两个零点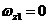 和 和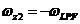 ,具有高通性。 ,具有高通性。 原点上的零点表示,如果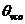 变化缓慢,则 变化缓慢,则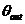 很小。因为在锁定条件下,VC0的相位变化通过PD变成了电压,加到VCO的控制输入端,使相位朝相反的方向变化。由于VCO的电压相位转变对缓慢变化的控制电压 很小。因为在锁定条件下,VC0的相位变化通过PD变成了电压,加到VCO的控制输入端,使相位朝相反的方向变化。由于VCO的电压相位转变对缓慢变化的控制电压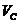 有无穷的增益,负反馈抑制了输出相位变化。 有无穷的增益,负反馈抑制了输出相位变化。 PLL可以简化为下图结构:一个理想的积分器位于负反馈环中,在输入端 产生了一个“虚地’,因此,对于缓慢变化的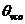 。,则 。,则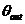 =0。 =0。 
3.1图简单的锁相环VCO噪声模拟 假设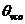 变化很快,则 变化很快,则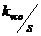 的大小,以及环路增益都相应减小,这样,也会使“虚地”产生变化。当 的大小,以及环路增益都相应减小,这样,也会使“虚地”产生变化。当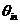 变化接近 变化接近 ,环路增益由于低通滤波器而减小。 ,环路增益由于低通滤波器而减小。 从公式(3.2)可知,当s→∞时,有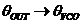 。即 。即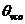 当变化非常快时环路相当于开环状态。 当变化非常快时环路相当于开环状态。 利用压控振荡器传递函数:,将电源加一个很小的阶跃q,则输出为: 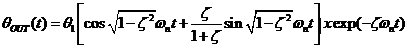 (3.3) (3.3)
由上式有时间常数为1/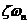 。为了使PLL有快的锁定特性,尽量将 。为了使PLL有快的锁定特性,尽量将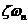 取大。 取大。 为了减小VCO的相位噪声的影响,环路带宽应该尽量取大,而这与抑制输入相位噪声将环路噪声带宽尽量减小相矛盾。实际工程中,输入信号主要来自晶体振荡器,噪声非常小,所以,PLL的输入相位噪声主要来自内部的VCO,因此可以将环路带宽适当取大。 3.3相位噪声的抑制 锁相环的抖动主要是由相位噪声或边带引起的。而产生随机抖动和相位噪声的原因,可以简单认为是电源噪声、衬底噪声和器件噪声。边带则基本上是由控制路径上的周期性扰动引起的。 结合实际,抖动产生的原因如有: 1.电源噪声和衬底噪声,引起了受电压影响的电容(如MOS管的Cgd)的变化,导致振荡器频率的变化。可以把电源和衬底也作为VCO的控制电压来分析VCO的频率特性; 2.衬底噪声,衬底噪声会导致器件阈值电压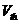 的改变; 的改变; 3.器件噪声(热噪声、闪烁噪声),闪烁噪声随着振荡器(VCO)的频率慢慢变化,它能够通过增加PLL的带宽来抑制。热噪声可以通过版图的方法减小。减小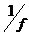 噪声要增加器件面积。 噪声要增加器件面积。 在PLL设计过程中,应当尽量遵循以下原则来减小抖动: 1.将缓冲控制电压(buffered control voltage)作为电源电压。 2.用缓冲控制电压去产生偏置电流,电流源隔离。 3.采用Cascode电流源或镜像电流源,可以将敏感性降到O.5%。 4.用阱器件来做电流源和环路滤波电容。 5.将控制电压做在阱上面(避免衬底的影响)。 3.4本章小结 本章对锁相环系统噪声进行了概括介绍,对锁相环系统的输入噪声,相位噪声给出了相关说明及减小噪声的一些措施,指出锁相环路设计中应该尽可能的减小噪声带来的影响,实际意义很重要。 第四章二阶锁相环仿真及结果 4.1仿真介绍 仿真使用的软件是MATLAB7.0。由于MATLAB仿真软件适合多学科、多种工作平台且功能强大、界面友好、方便快捷、语言自然并且开放性强的大型优秀应用软件,已经也已成为国内外高等院校高等数学、数值分析、数字信号处理、自动控制理论以及工程应用等课程的基本教学工具。使用Matlab对锁相环仿真的实现是方便快捷的。 仿真所采有的是二阶锁相环。这是由于我们实际应用中的绝大多数PLL,或者是二阶的,或者是通过忽略高阶效应(至少在初步设计时)而被设计成近似的二阶环路。鉴于二阶锁相环在实际应用的意义,所以在仿真采用了二阶锁相环。
- % File: c6_nltvde.m
- w2b=0; w2c=0; % initialize integrators
- yd=0; y=0; % initialize differential equation
- tfinal = 50; % simulation time
- fs = 100; % sampling frequency
- delt = 1/fs; % sampling period
- npts = 1+fs*tfinal; % number of samples simulated
- ydv = zeros(1,npts); % vector of dy/dt samples
- yv = zeros(1,npts); % vector of y(t) samples
- %
- % beginning of simulation loop
- for i=1:npts
- t = (i-1)*delt; % time
- if t<20
- ydd = 4*exp(-t/2)-3*yd*abs(y)-9*y; % de for t<20
- else
- ydd = 4*exp(-t/2)-3*yd-9*y; % de for t>=20
- end
- w1b=ydd+w2b; % first integrator - step 1
- w2b=ydd+w1b; % first integrator - step 2
- yd=w1b/(2*fs); % first integrator output
- w1c=yd+w2c; % second integrator - step 1
- w2c=yd+w1c; % second integrator - step 2
- y=w1c/(2*fs); % second integrator output
- ydv(1,i) = yd; % build dy/dt vector
- yv(1,i) = y; % build y(t) vector
- end % end of simulation loop
- plot(yv,ydv) % plot phase plane
- xlabel('y(t)') % label x axis
- ylabel('dy/dt') % label y zxis
- % End of script file.
- % File: pllpost.m
- %
- kk = 0;
- while kk == 0
- k = menu('Phase Lock Loop Postprocessor',...
- 'Input Frequency and VCO Frequency',...
- 'Input Phase and VCO Phase',...
- 'Frequency Error','Phase Error','Phase Plane Plot',...
- 'Phase Plane and Time Domain Plots','Exit Program');
- if k == 1
- plot(t,fin,'k',t,fvco,'k')
- title('Input Frequency and VCO Freqeuncy')
- xlabel('Time - Seconds');ylabel('Frequency - Hertz');pause
- elseif k ==2
- pvco=phin-phierror;plot(t,phin,t,pvco)
- title('Input Phase and VCO Phase')
- xlabel('Time - Seconds');ylabel('Phase - Radians');pause
- elseif k == 3
- plot(t,freqerror);title('Frequency Error')
- xlabel('Time - Seconds');ylabel('Frequency Error - Hertz');pause
- elseif k == 4
- plot(t,phierror);title('Phase Error')
- xlabel('Time - Seconds');ylabel('Phase Error - Radians');pause
- elseif k == 5
- ppplot
- elseif k == 6
- subplot(211);phierrn = phierror/pi;
- plot(phierrn,freqerror,'k');grid;
- title('Phase Plane Plot');xlabel('Phase Error /Pi');
- ylabel('Frequency Error - Hertz');subplot(212)
- plot(t,fin,'k',t,fvco,'k');grid
- title('Input Frequency and VCO Freqeuncy')
- xlabel('Time - Seconds');ylabel('Frequency - Hertz');subplot(111)
- elseif k == 7
- kk = 1;
- end
- end % End of script file.
- % File: pllpre.m
- %
- clear all % be safe
- disp(' ') % insert blank line
- fdel = input('Enter the size of the frequency step in Hertz > ');
- fn = input('Enter the loop natural frequency in Hertz > ');
- lambda = input('Enter lambda, the relative pole offset > ');
- disp(' ')
- disp('Accept default values:')
- disp(' zeta = 1/sqrt(2) = 0.707,')
- disp(' fs = 200*fn, and')
- disp(' tstop = 1')
- dtype = input('Enter y for yes or n for no > ','s');
- if dtype == 'y'
- zeta = 1/sqrt(2);
- fs = 200*fn;
- tstop = 1;
- else
- zeta = input('Enter zeta, the loop damping factor > ');
- fs = input('Enter the sampling frequency in Hertz > ');
- tstop = input('Enter tstop, the simulation runtime > ');
- end %
- npts = fs*tstop+1; % number of simulation points
- t = (0:(npts-1))/fs; % default time vector
- nsettle = fix(npts/10); % set nsettle time as 0.1*npts
- tsettle = nsettle/fs; % set tsettle
- % The next two lines establish the loop input frequency and phase
- % deviations.
- fin = [zeros(1,nsettle),fdel*ones(1,npts-nsettle)];
- phin = [zeros(1,nsettle),2*pi*fdel*t(1:(npts-nsettle))];
- disp(' ') % insert blank line
- % end of script file pllpre.m
- % File: pll2sin.m
- w2b=0; w2c=0; s5=0; phivco=0; %initialize
- twopi=2*pi; % define 2*pi
- twofs=2*fs; % define 2*fs
- G=2*pi*fn*(zeta+sqrt(zeta*zeta-lambda)); % set loop gain
- a=2*pi*fn/(zeta+sqrt(zeta*zeta-lambda)); % set filter parameter
- a1=a*(1-lambda); a2 = a*lambda; % define constants
- phierror = zeros(1,npts); % initialize vector
- fvco=zeros(1,npts); % initialize vector
- % beginning of simulation loop
- for i=1:npts
- s1=phin(i) - phivco; % phase error
- s2=sin(s1); % sinusoidal phase detector
- s3=G*s2;
- s4=a1*s3;
- s4a=s4-a2*s5; % loop filter integrator input
- w1b=s4a+w2b; % filter integrator (step 1)
- w2b=s4a+w1b; % filter integrator (step 2)
- s5=w1b/twofs; % generate fiter output
- s6=s3+s5; % VCO integrator input
- w1c=s6+w2c; % VCO integrator (step 1)
- w2c=s6+w1c; % VCO integrator (step 2)
- phivco=w1c/twofs; % generate VCO output
- phierror(i)=s1; % build phase error vector
- fvco(i)=s6/twopi; % build VCO input vector
- end
- % end of simulation loop
- freqerror=fin-fvco; % build frequency error vector
- % End of script file.
- function [] = pplane(x,y,nsettle)
- % Plots the phase plane with phase in the range (-pi,pi)
- ln = length(x);
- maxfreq = max(y);
- minfreq = min(y);
- close % Old figure discarded
- axis([-1 1 1.1*minfreq 1.1*maxfreq]); % Establish scale
- hold on % Collect info for new fig
- j = nsettle;
- while j < ln
- i = 1;
- while x(j) < pi & j < ln
- a(i) = x(j)/pi;
- b(i) = y(j);
- j = j+1;
- i = i+1;
- end
- plot(a,b,'k')
- a = [];
- b = [];
- x = x - 2*pi;
- end
- hold off
- title('Phase-Plane Plot')
- xlabel('Phase Error / Pi')
- ylabel('Frequency Error in Hertz')
- grid % End of script file.
- % File: ppplot.m
- % ppplot.m is the script file for plotting phase plane plots. If the
- % phase plane is constrained to (-pi,pi) ppplot.m calls pplane.m.
- kz = 0;
- while kz == 0
- k = menu('Phase Plane Options',...
- 'Extended Phase Plane',...
- 'Phase Plane mod(2pi)',...
- 'Exit Phase Plane Menu');
- if k == 1
- phierrn = phierrn/pi;
- plot(phierrn,freqerror,'k')
- title('Phase Plane Plot')
- xlabel('Phase Error /Pi')
- ylabel('Frequency Error - Hertz')
- grid
- pause
- elseif k == 2
- pplane(phierrn,freqerror,nsettle+1)
- pause
- elseif k == 3
- kz = 1;
- end end % End of script file.
4.3仿真结果 图4.1 锁相环处理框 上图是利用MATLAB提供的函数将计算结果图形化功能建立的。在运行程序后,就会出现上面的对话框,点击点击其中的任何一项就会出现相应的仿真图形。上图中包含了输入频率和VCO频率,输入相位和VCO相位,频率误差,相位误差,相位空间波特图,相位空间和时域,退出程序等选项。 运行程序后出现如下指令: Accept the tentative values: the first loop frequency is 5 第一循环频率 Enter y for yes or n for no > y Enter the loop gain >40 输入环路增益为40 Enter the sampling frequency in Hertz > 1200 输入采样频率 Enter tstop, the simulation runtime > 5 仿真时间为5秒 设置好参数后运行程序,由上我们可知环路增益为40,仿真时间为5s,采样频率为1200Hz。接着点击上图4.1中的菜单,就能得到如下仿真图像。其中我们主要观察输入相位和VCO相位。 图4.2 输入相位和VCO相位 图4.3 相位误差图 图4.2中蓝线为输入相位,绿线代表VCO相位,从图中可以看见随着时间的变化输入信号相位为线性,而VCO相位则是经历了一段曲线后斜率与输入信号相位斜率相同,输出相位跟随输入相位,达到稳定。图4.3中VCO的相位也是先经历了一段时间的曲线后变为一条直线达到稳定。根据锁相环的基本原理我们可知锁相环是个反馈网络,它是由输出信号(VCO产生)与参考频率在频率和相位上保持同步或者保持常数。由此我们可以看出锁相环工作后,在最初的一段时间中锁相环开始工作,输入信号经过鉴相器,环路虑波器后,将输出相位反馈给VCO压控振荡器,使压控振荡器与输入频率逐步实现同步,保持一个常数,实现锁定。其中经历了锁相环的失锁、跟踪、捕获、锁定,从而达到最后达到稳定状态。从开始到达到稳定的这段时间则为做捕获时间。 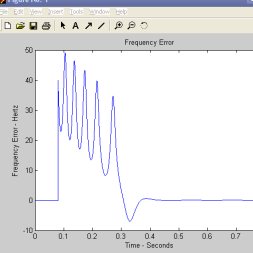 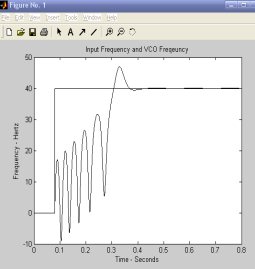 图4.4 频率差图 图4.5 输入频率和VCO频率图 图4.4 频率差图 图4.5 输入频率和VCO频率图
图4..4与图4.5也显示了锁相环工作后从失锁、跟踪、捕获、锁定的过程,过程。从不停的摆动到最后的直线状态,这个过程称为锁定过程。其中我们可以发现在捕捉过程中随着捕捉次数的增加,捕捉过程也变得较慢,这说明此时的的锁相环工作平率处在稳定工作的动态界限内,工作正常。 4.4本章小结 本章介绍了仿真的环境以及二阶锁相环的仿真过程,并对其仿真结果进行了分析。在前三章的理论基础上,通过使用MATLAB7.0进行了仿真。实验结果表明:用MATLAB进行的二阶锁相环仿真达到了最初的设想,锁相环的失锁、跟踪、捕获、锁定各个阶段均有体现。达到了最初仿真的要求。 结 论 本文在阅读一些文献和对锁相环有一定程度了解的基础上,运用MATLAB进行了仿真。本文完成了以下工作: - 在掌握了锁相环的基本原理并对文献研究的基础上,对锁相环的工作原理进行了深入的分析,深入了解锁相环技术的数学分析方法,应用此方法得到锁相环技术的数学模型,用这些理论指导实际中的设计工作。
- 在对基本原理和电路结构确定的基础上,将锁相环的整体电路进行层次化分解,即鉴频鉴相器、低通滤波器、压控振荡器,并对各个模块的工作原理和性能进行了比较详细的分析。
- 用MATLAB软件对设计的锁相环电路进行了模拟仿真,验证了电路功能的正确与否,以及锁相环的设计目标是否达到。
由于时间和条件的限制,在设计工作中有些工作没有做到,留待进一步的完善,后续工作是: - 在运用MATLAB设计锁相环时,并没有引入噪声对锁相环的影响及相应的分析,也未对锁相环的各项参数进行深入的讨论。
- 仅限于对锁相环理论的研究与分析上,并没有针对其实际中的应用研究相关的了解。
- 在此次仿真中只对二阶锁相环进行了仿真,并没有对其他锁相环进行仿真和研究,也没有进行硬件实现。
目前锁相环技术在通信中早已成熟,随着科技的发展,目前的锁相环都是基于半导体工艺的集成电路。对于未来而言,用锁相环的集成化设计减小相应噪声、提高锁相环的频率预测精度、硬件系统的运算速率以及降低干扰也是其研究的一个重要方向。
完整的Word格式文档51黑下载地址:
 锁相环与MATLAB仿真.doc
(508 KB, 下载次数: 50)
锁相环与MATLAB仿真.doc
(508 KB, 下载次数: 50)
|