|
粘贴过来的代码都乱了,贴个原文链接吧: https://blog.csdn.net/D_SEngineer?spm=1011.2124.3001.5113 不定时发送福利,欢迎小伙伴们交流学习。
上一节对PID三个参数进行了分析,知道了三个参数各自的优缺点,这节我们将三个参数整合到一起,通过他们之间优缺点互补,真正形成一个稳定的系统。 PID雏形将上一小节的公式相加: OUT = OUTp + OUTi + OUTd = K*Ek + K*Sk + K*Dk + 3*OUT0 = K*(Ek +Sk +Dk)+ OUTx式子中3*OUT0为常数,用常数OUTx代替。 模拟PID到离散型PID的转换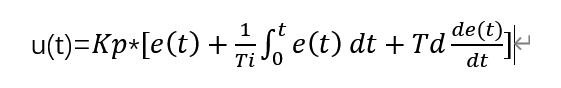
这是模拟PID公式,对于这个公式,你要知道:
Kp :放大系数
e(t):误差(t代表第t时刻采样得到的误差)
Ti :积分时间常数
Td:微分时间常数 另外一点就是,我们使用单片机进行PID运算,是不能采用模拟型PID的,因为单片机本身就是一个数字系统,里面只有0和1,因此不能处理模拟信号,只能将模拟信号转换成数字信号,才能被单片机所用。
因此上面的公式不能使用,需要稍稍变动。 那么怎么转换呢? 1. 比例项: 比例项就不同看了,很简单,误差乘上系数就行了,主要是积分项和微分项、 2. 积分项: 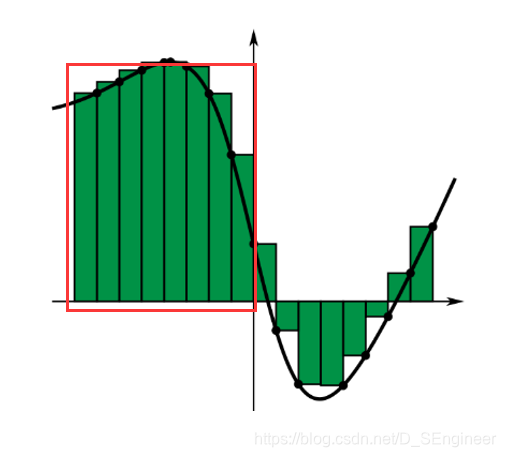
高数中是不是有一张和这个图很像的一张图,应该在微积分那一章中,是让求不规则图形面积的。上图红色框内,黑色曲线的面积是怎么求的?是不是将黑线拆分成很多个矩形,把这些矩形面积相加就行了。这个理念和离散型PID很像,我们定时去采样,之后把采样值进行PID计算,这个时间越小,离散型的结果就越接近模拟型结果。
那么积分项就可以写成下面的公式:
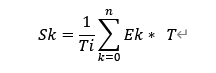
Sk:是积分输出项
Ek:表示误差(第k次采样的误差)
T:采样时间
Ti:积分常数 公式可以这样理解:
将误差看做坐标轴的Y轴(长),T看做X轴(宽),当k=1时,表示第一次采样的误差E1×采样时间T是不是相当于求矩形的面积(长×宽),之后将所有的矩形面积都累加起来,就可以近似求出曲线的面积。 3. 微分项
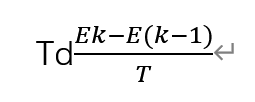 积分是无限累加,微分是无限分割,Ek和Ek-1还看做Y轴,T是X轴。斜率 =(y2-y1)/(x2-x1),(y2-y1)就是Ek - Ek-1,(x2-x1)就是T。当采样时间T足够小时,上面这个公式是不是可以看成曲线上每个点(甚至更小)的效率了。 最终离散型公式: 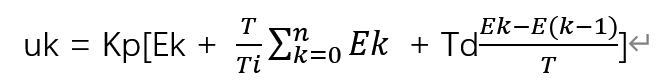
离散型PID公式中的几个参数总结- 积分时间常数Ti
(1)T是采样时间,Ti是积分时间常数,两个不一样,最终积分系数Ki=Kp*(T/Ti)
(2)Ti在分母上,因此Ti越大,Ki越小,积分作用越小;Ti越小,Ki越大,积分作用越大
(3)我们最终调节的参数是合并之后的Ki,而不会单独调节Ti - 微分时间常数Td.
(1)Td越大,积分作用就越大,Td越小,积分作用就越小
(2)我们最终调节的参数是合并之后的Kd,而不会单独调节Td
PID注意事项假设是温控系统,我们设定目标值为100℃,当第一次采样到第一到达目标值时,误差Ek=Sv-Pk,该段时间内的误差都为正数,积分项是将所有误差都累加起来的,因此在第一次到达目标值时,会累积很大一个误差,该误差会造成即便温度达到目标值100℃,此时P项没有作用了,但系统还是会继续加热,为什么?就是因为此时积分项经过计算,会输出一个很大的值。这就造成系统产生过冲,最直观的表现就是下图中,第一次超过目标值产生的过冲现象。
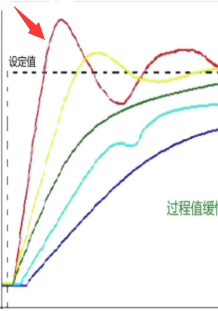
解决办法就是一开始不加入积分项,当温度到达一定值,比如80℃时,在加入积分项。 这种情况一般会出现在系统启动、结束或大幅度增减设定值时,短时间内会造成系统输出很大的偏差,这种情况可以采用上述方法(积分分离)来解决。
|