倒立摆是一个典型的多变量、非线性、强耦合、欠驱动的自然不稳定系统,对倒立摆系统的控制研究,能反映控制过程中的镇定、非线性和随动等问题,因此常用于各种控制算法的研究。
本次课设我以直线二级倒立摆系统为模型,阐释了直线二级倒立摆的建模方法和镇定控制算法。其次介绍了直线二级倒立摆系统的结构和参数,应用拉格朗日方程建模方法详细推导了二级倒立摆的数学模型,并对系统的性能进行分析。接下来,本文重点研究了最优控制算法在直线二级倒立摆镇定控制中的应用;在介绍倒立摆系统的最优控制算法的基础上,设计了系统的最优控制器,分析得出控制参数的选择规律;并且在Simulink上完成仿真实验,观察控制系统性能。
倒立摆是进行控制理论研究的典型实验平台,许多抽象的控制理论概念,如系统的稳定性、可观性及可控性等都可以通过该系统直观地表示出来。因此,近几年来,该系统已经成为控制领域的研究热点。 倒立摆系统是一个典型的非线性、强耦合、多变量和不稳定系统。在控制研究领域有着代表性的意义。倒立摆作为控制系统的被控对象,许多抽象的控制概念都可以通过它直观的表现出来。本次课设我选用以二级倒立摆为研究对象,采用牛顿力学定律进行数学建模,利用二次型最优控制器( LQR)求出最优状态反馈矩阵K,经过对Q和R两个加权矩阵的选取实现二级倒立摆的自动控制。该方法为多变量反馈系统的设计提供了有效的分析法,可适于时变系统,处理扰动信号和测量噪声,处理有限和无限的时间区间。
1 系统建模 1.1相关数据 为简化系统,我们在建模时忽略了空气阻力和各种摩擦,并认为摆杆为刚体。 二级倒立摆的组成如图 1 所示: 图 1 直线两级倒立摆物理模型 首先,对该系统做如下假设: 1)小车、一级摆杆和二级摆杆都是刚体。 2)皮带轮与同步带之间无相对滑动,且同步带不会拉伸变长。 3)小车与导轨之间的摩擦力与小车速度成正比。 4)各级摆杆与转轴间的转动摩擦力矩与摆杆的角速度成正比。 表1 二级倒立摆各物理参数:
1.2理论依据 1.2.1 受力分析 利用拉格朗日方程推导运动学方程: 拉格朗日方程为: 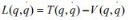 (1-1) 其中 L 为拉格朗日算子,q 为系统的广义坐标,T 为系统的动能,V 为系统的 势能。 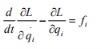 (1-2) 其中 i=1,2,3……n, i f 为系统在第 i 个广义坐标上的外力,在二级倒立摆系统中,系统的广义坐标有三个广义坐标,分别为 x, θ1, θ2 。 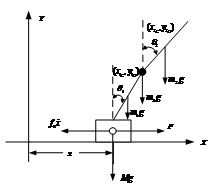
图2 直线二级倒立摆受力分析 先对倒立摆的物理模型进行分析,如图2所示,然后建立摆杆和质量块的质心的坐标表达式。这里规定摆杆1的质心坐标为 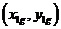 ,摆杆2的质心坐标为 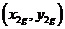 ,质量块的质心坐标为 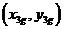 。质心坐标如下: 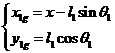
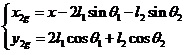 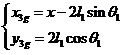
在直线二级倒立摆系统中,广义坐标为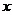 , ,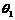 和 和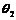 。根据倒立摆的物理模型分析图,列写出系统的动能为: 。根据倒立摆的物理模型分析图,列写出系统的动能为: 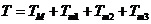 (1-3) (1-3) 其中, 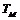 、 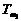 、 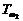 和 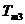 分别为小车、摆杆1、摆杆2和质量块1的动能,它们分别为: 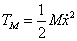 (1-4) 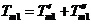 (1-5) 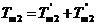 (1-6) 其中, 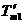 和 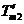 分别为摆杆1和摆杆2质心平动动能, 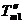 和 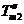 分别为摆杆1和摆杆2绕质心转动动能。然后,应用摆杆和质量块质心表达式求出系统的动能。 将质心坐标带入公式(1-6)摆杆1的动能为: 所以得到 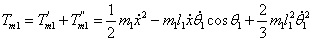 (1-7) 同理带入(1-7),求出摆杆2的动能为: 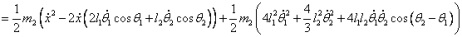 (1-8) 同理带入(1-5),质量块1的动能为: 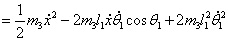 (1-9) 因此将(1-7)(1-8)(1-9)带入(1-3),可以得到系统动能为 另一方面,系统的势能为 从而得到Lagrange函数为 1.2.2 列出Lagrange方程 由于在广义坐标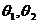 上均无外力作用,故列写Lagrange方程得到 上均无外力作用,故列写Lagrange方程得到 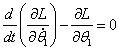 (2-1) 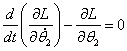 (2-2) 将L代入式(2-1)和(2-2)得到 上述方程为倒立摆的动力学方程,求解微分方程可以得到倒立摆状态量 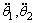 的表达式,然后可以建立倒立摆的数学模型。
1.3 倒立摆运动方程的线性化处理 针对已建立的拉格朗日方程,求解方程可以得到倒立摆状态量 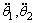 的表达式。由于 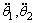 是关于系统的状态变量和输入控制量u的方程,小车施加的加速度信号作为控制量,有 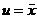 ;因此设方程的解为: 对倒立摆模型进行线性化处理,这里采用在平衡点附近将函数进行泰勒级数展开。上面的方程为七元函数,因此采用对多元函数展开的方法展开,这里对二元函数的泰勒级数展开方法进行介绍。 二元函数的形式为 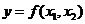 ,在其平衡点 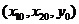 附近进行泰勒级数展开。在平衡点附近,由于偏差 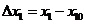 及 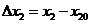 的绝对值很小,可以省略函数高次项得: 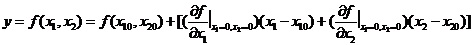 (3-1) 将上式化简,得到一次线性方程: 这样, 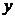 与 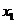 和 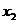 之间的非线性关系,转化为 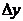 与 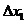 和 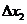 之间的线性关系。当系统的平衡点处于原点时,即 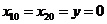 ,可以对方程化简为: 按照二元函数的泰勒级数展开方法对公式(3-1)进行展开,由于直线二级倒立摆系统的平衡点为: 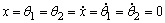 ;因此线性化后得到 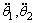 的表达式为: 其中 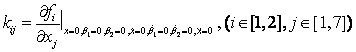 由于求解微分方程比较繁琐,因此对线性化处理后的方程采用mathematica软件编写程序,求解倒立摆状态量 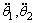 的表达式。根据得到的参数,建立倒立摆的数学模型。
运行程序求出倒立摆状态量 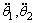 的表达参数 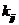 ,其中k11、k14、k15、k16、k21、k24、k25、k26的值为0,其余各参数的表达式如下: (g取10N/kg,M=1.32kg,m1=0.04kg ,m2=0.132kg,m3=0.208kg,l1=0.09m,l2=0.27m) 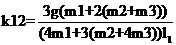 =78.64; 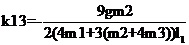 =-21.62; 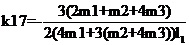 =5.70; 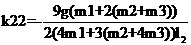 =-39.32; 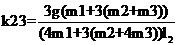 =38.59; 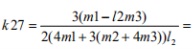 -0.029; 对二级倒立摆系统,取系统状态变量为 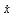  [1],然后建立连续状态空间方程为: 根据系统状态变量直接的关系,写出系统的状态空间方程为:
1.4 能控能观性检测 1.4.1能控性检测 QC=rank[B A*B A^2*B A^3*B A^3*B A^4*B]=6=n 完全能控 1.4.2观测性检测 UO=rank[C A*C A^2*C A^3*C A^3*C A^4*C]=6=n 完全能观
2 模糊控制器的设计 2.1模糊控制器基本原理 模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础的一种智能控制方法,它是从行为上模仿人的模糊推理和决策过程的一种智能控制方法。该方法首先将操作人员或专家经验编成模糊规则,然后将来自传感器的实时信号模糊化,将模糊化后的信号作为模糊规则的输入,完成模糊推理,将推理后得到的输出量加到执行器上。 简言之,模糊控制器会将输入的误差和误差变化量的精确值进行模糊化,然后将模糊值进行逻辑推理,最后将得到的模糊值去模糊化再送出。 模糊控制器的结构如图3所示。控制器由4个基本部分组成,即模糊化接口、知识库、推理机、解模糊接口。 根据前面介绍的二级倒立摆稳定控制思想,采用融合技术设计一个线性融合函数,把多个变量融合成为综合误差E和综合误差变化率EC,这就可以使模糊控制器的设计大为简化。如图4。 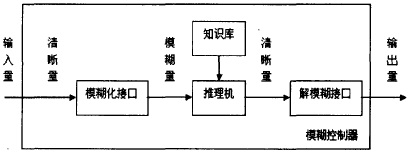
图3模糊控制器的结构 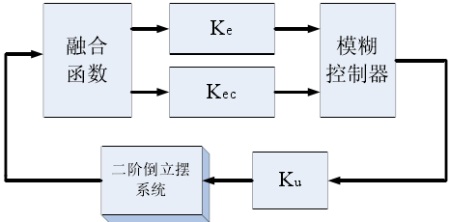
图4 采用融合技术的模糊控制器 2.2模糊控制器设计步骤 (1)确定模糊控制器的输入变量和输出变量(即控制量); (2)设计模糊控制器的控制规则; (3)进行模糊化和解模糊化; (4)选择模糊控制器的输入变量及输出变量的论域,并确定模糊控制器的参数(如量化因子、比例因子); (5)编制模糊控制算法的应用程序; 2.3模糊规则表

If EC=NB and E=NB then U=NB ; If EC=NB and E=NM then U=NB If EC=NB and E=NS then U=NB If EC=NB and E=ZE then U=NM If EC=NB and E=PS then U=NM If EC=NB and E=PM then U=NS If EC=NM and E=NB then U=NB …… 2.4利用融合函数设计 基于LQR理论来为二级倒立摆的状态方程设计一个状态反馈矩阵K和降维矩阵G,将六个状态变量综合成两个变量,即综合误差E和综合误差变化率EC。并通过LQR仿真,得出输入输出数据对,根据得出的数据,计算并制定出模糊规则。 利用最优控制理论计算出一组可以让二级倒立摆稳定的状态反馈矩阵K: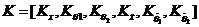 (2-1) (2-1) 最优控制性能指标函数为: 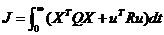 (2-2) (2-2)
通过使性能指标函数式(6-1)为最小,可求得: 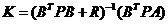 (2-3) (2-3)
求解如下Ricatti方程可得到矩阵P。 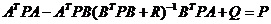 (2-4) (2-4)
性能指标函数中,矩阵Q和矩阵R这两个参数需要定义,是用来平衡系统对输入量和状态量的敏感程度的。它们对闭环系统的动态性能影响很大。在倒立摆系统中,Q,R分别用来对状态向量X和输入控制量u进行平衡加权的。一般情况下,R增加时,控制力减小,角度变化变小,跟随速度变慢。而Q中某元素增加时,其对应的状态变量的响应速度增加,其它状态变量的响应速度相对减慢。为了使得反馈矩阵K更合理,对矩阵Q, R的选取一定要尽量恰当。通过反复的测试,在实际系统的控制过程中,选取 
基于MATLAB强大的矩阵运算以及它丰富的内部函数,利用K=lqr(A,B,Q,R)命令通过计算,可得到状态反馈矩阵K: K=[17.3205,111.7009,-200.6791,18.6848, 2.6899,-32.5784] 本文应用归一化思想设计降维矩阵G。从上面的结论中得知状态矩阵K中包含六个元素,分别代表着六个状态变量的权值。根据归一化思想,每个元素均除以矩阵K的范数,为了把六个状态变量合并成两个变量,设计如式(2-5 )形式的矩阵,利用状态反馈阵K构造出降维矩阵G: 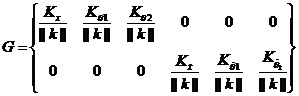 (2-5) (2-5)
其中,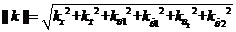 把所得状态反馈阵K的值代入式(6-5 )得到G: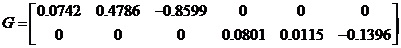 最后,通过降维矩阵G把六个状态变量X综合为两个变量,称为综合误差E和综合误差变化率EC。 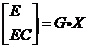 (2-6) (2-6)
2.5模糊控制器的输入输出论域及模糊集合的划分 首先对系统进行采样,粗略确定输入输出论域:位置[-0.2,0.2],速度[-1,1],下摆角[-0.15,0.15],下摆角速度[-4 , 4]上摆角[-0.08, 0.08],上摆角速度[-0.8, 0.8],控制力[-45,45]。为简化,综合误差E、综合误差变化域EC和输出量化域均为[-3,3]。 可大致估算E的量化因子为14,EC的量化因子为18,U的的比例因子为15。
3 matlab仿真 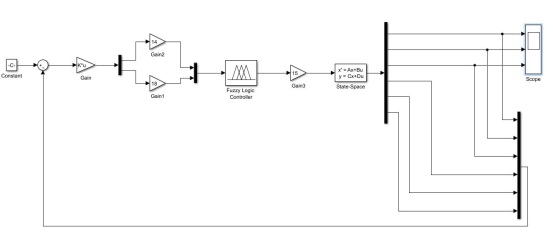
图5 模型建立 该模型Constant初值我设定为0,融合矩阵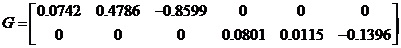 ,系统矩阵A= ,系统矩阵A= ,输入矩阵B= ,输入矩阵B=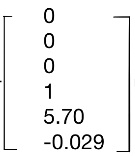 , , 输出矩阵C= ,直联矩阵D= ,直联矩阵D= 。初始,我选定E的量化因子为14,EC的量化因子为18,U的的比例因子为15。 。初始,我选定E的量化因子为14,EC的量化因子为18,U的的比例因子为15。
图5.误差E 图6.误差率EC 图7.模糊控制对应规则 (规则详参) 表3 模糊规则表
If EC=NB and E=NB then U=NB ; If EC=NB and E=NM then U=NB If EC=NB and E=NS then U=NB If EC=NB and E=ZE then U=NM If EC=NB and E=PS then U=NM If EC=NB and E=PM then U=NS If EC=NM and E=NB then U=NB …… 图8 仿真波形(E的量化因子ke为14,EC的量化因子kec为18,U的的比例因子ku为15) 通过波形可以清楚的看到,在选取E的量化因子为14,EC的量化因子为18,U的的比例因子为15后,整个倒立摆系统大概在2秒钟略多一点,不到三秒钟的时候达到稳定状态,即两杆竖直倒立不动,小车不再有位移。
图8 仿真波形(E的量化因子ke为14,EC的量化因子为18,ku的的比例因子为20) 仔细观察仿真波形图,可以看到,比例因子增大,整个系统达到稳定的时间变长了。  图9 仿真波形(E的量化因子ke为10,EC的量化因子kec为18,U的的比例因子ku为20) 整个系统所需稳定时间拉长。 图10 仿真波形(E的量化因子ke为14,EC的量化因子kec为18,U的的比例因子ku为15) 该图在10s后添加了脉冲扰动信号。
结合翻阅资料可得,量化因子ke及kec 的大小对控制系统的动态性能影响很大,ke 选得较大时,系统的超调量也较大,过渡过程也较长。这一点也并不难理解,因为从理论上讲,ke 增大,相当于缩短了误差的基本论域,增大了误差变量的控制作用,虽然能使上升时间变短,但由于超调过大,使得系统的过渡过程变长。kec 选择越大系统超调越小,但系统的响应速度变慢,kec 对超调的遏制作用十分明显。
其中,ke 对动态性能的影响是:ke 越大,调节死区越小,上升速率越大,调节时间越长,超调量越大,但是,ke 取得过大,将使系统产生较大的超调,调节时间增大,甚至产生震荡,使系统不能稳定工作;而ke 过小,又使系统上升速率较小,系统调节隋性变大,同时也影响系统的稳态性能,使稳态精度降低。
kec对动态性能的影响是:kec大,反应较迟钝,调节时间短,超调量大;kec 小,反应快,上升速率小,调节时间长,超调量小;而kec过小,将引起调节时间过长,严重时系统不能稳定工作。
对系统稳定性的影响在模糊控制系统中,一般不可能消除稳态误差,更不可能消除误差变化率。一般而言,ke 增加,稳态误差将减小;kec 增大,稳态时误差变化率也将减小。然而ke 、kec 对动态性能也有影响,因此必须兼顾两方面的性能。
ku相当于常规系统中的比例增益,它主要影响控制系统的动态性能。一般ku增大,上升速率就快,超调量增大,响应时间减小,但是ku 过大,会导致系统输出上升速率过大,从而产生过大的超调乃至振荡和发散,严重时会影响稳态工作;而ku 过小,系统的前向增益很小,系统输出上升速率较小,快速性变差,稳态精度变差,和一般控制系统不同的是,ku 一般不影响系统的稳态误差。
同时应该指出,量化因子和比例因子的选择并不是唯一的,可能有几组不同的值,都能使系统获得较好的响应特性。对于比较复杂的被控过程,有时采用一组固定的量化因和比例因子难以收到预期的控制效果,可以在控制过程中采用改变量化因子和比例因子的方法,来调整整个控制过程中不同阶段上的控制特性,使其对复杂过程控制受到良好的控制效果。
以上的图文Word格式文档51黑下载地址:
|