' Bascom的迷你矩阵代数代码
' 加法、减法、乘法、倒置
' (Natalius Kiedro,2010年3月)
'我错过了矩阵代数的学习,因为最近我在使用AVR系列(参见我之前关于这个问题的帖子)时遇到了一个需要用到‘矩阵乘法’的问题。
'20年前,我通过编写一个程序来玩转矩阵,这个程序可以在电脑屏幕上绘制并旋转生物分子的3D图像。那个
'时期的另一个项目是关于动力学数据的动态模拟和非线性数据拟合。像3D旋转和参数优化这类事情,在很大
'程度上都依赖于矩阵代数。下面是一个关于矩阵的简要介绍,互联网上有成千上万页的资料可以提供更多信息。
'矩阵入门简介’
'===============
'矩阵是一个数字表。在大多数情况下,数字以类似正方形的形式排列,如下所示:
' | A(1,1) A(1,2) A(1,3) | | 1 2 3 |
'矩阵A = | A(2,1) A(2,2) A(2,3) | = | 4 5 6 | 是一个3x3矩阵
' | A(3,1) A(3,2) A(3,3) | | 7 8 9 |
'矩阵中的数字A(i,j)被称为矩阵的元素。元素A(1,1)的值为1,元素A(2,3)的值为6,以此类推。
'变量i和j是矩阵的索引,i指向行,j指向列,元素就位于该行和该列的交叉点上。
'现在,让我们来看看普通代数。我们有四个每个人都喜欢使用的基本运算:
'加法:C = A + B
'减法:C = A - B
'乘法:C = A * B
'除法:C = A / B
'它们在矩阵代数中的等价运算分别被称为矩阵加法、矩阵减法、矩阵乘法,以及——哎呀——没有所谓的矩阵除法。
'在矩阵代数中,除法是分步进行的。让我们用普通代数来演示一下,看看它在矩阵代数中是如何进行的:
'C = 1 / B:在矩阵代数中,我们称之为矩阵求逆。
'C = C * A:这是矩阵乘法。
'因此,C = 1 / B * A = A / B(在矩阵代数中,这种表示并不严谨,仅用于说明概念)
'所以,在矩阵代数中,除法并不是一个基本运算,因为它可以分解为矩阵求逆和矩阵乘法。
'在普通代数中,数字1是特殊的,因为:
'C = C * 1:(当然,纳塔利乌斯,我们都知道这一点!)
'C = C / 1:(拜托,纳塔利乌斯,你想让我们觉得无聊吗,巴斯科默?)
'不,我不想让任何人觉得无聊。我只是想和你分享矩阵的乐趣!就像尼奥几年前做的那样。
'让我们重新加载这个矩阵,它是……的等价物(此处原文被截断,但根据上下文,可以推测“
'它是……的等价物”可能是指矩阵运算在某种情况下的应用或等价表示)。
'数字1的特殊性在于:
'| 1 0 0 |
'| 0 1 0 | 它被称为单位矩阵,也有人称之为
'| 0 0 1 | 统一矩阵——当然,还有像我这样的人喜欢称之为单位矩阵。
'从矩阵的1,1,1路径穿过的线被称为矩阵的对角线。元素0被称为非对角元素。单位矩阵的特别之处在于,
'其对角线上的元素全部为1,而非对角线上的元素全部为0。
'为什么数字1和单位矩阵如此特殊呢?
'想象一下,如果在Bascom中无法使用乘法和除法,而你需要从零开始,在汇编语言中自己编写这些运算的代码。
'你会如何证明你的算法是有效的呢?
'最简单的方法就是将你的输入数字乘以1或除以1,然后观察数字是否保持不变——正如预期的那样。
'因此,如果我们将这个原理应用到矩阵代数中,我们期望:
'矩阵A乘以单位矩阵 = 矩阵A
'如果矩阵乘法的算法是有效的。如果:
'矩阵A乘以矩阵A的逆矩阵 = 单位矩阵
'那么我们就知道我们的矩阵求逆算法是有效的。很简单,对吧?
'Bascom中的矩阵代数
'========================
'矩阵代数通常使用二维数组进行计算,但Bascom并不了解二维数组。而且它也不需要了解,
'因为汇编语言总是将计算机内存视为线性(一维)排列的。让我们回顾一下本教程开头给出的二维矩阵排列的例子。
'在Bascom中,我们将二维矩阵当作一维矩阵来处理。因此,矩阵A变为:
'矩阵A = |A(1,1) A(1,2) A(1,3) A(2,1) A(2,2) A(2,3) A(3,1) A(3,2) A(3,3)|
'= | 1 2 3 4 5 6 7 8 9 |
'= | A(1) A(2) A(3) A(4) A(5) A(6) A(7) A(8) A(9)|
'为了将针对二维矩阵编写的矩阵代数运算转换为适用于“Bascom化”的一维矩阵的运算,
'我们只需将元素A(i,j)的索引i,j转换为一个指向第ij个元素A(ij)(即A(1)至A(9))的单索引ij。
'这非常简单:以下是一个只执行此操作的“空”矩阵循环:
'Dim I As Byte, I0 As Byte, J As Byte, Ij As Byte, N As Byte
' N是矩阵的大小。对于3x3矩阵,N为3;对于NxN矩阵,N为相应的值
'N = 3
'For I = 1 TO N '1, 2, 3
'I0 = I - 1 '0, 1, 2
'I0 = I0 * N '0, 3, 6(计算当前行之前所有行的元素总数)
'For J = 1 TO N '例如,当I=2时,I0=3,则J=1,2,3
'Ij = I0 + J '计算一维数组中的索引位置,即4, 5, 6
'Next J
'Next I
'断线内为AI给出的释义:
'////////////////////////////////////////////////////////////////////////////////////////////////////////////
'在矩阵程序中,变量通常用于表示矩阵的维度、索引位置以及辅助计算。以下是对您提供的代码中各个变量的具体含义的解释:
' N As Byte:
'含义:N代表矩阵的大小,即矩阵的行数和列数。对于NxN矩阵,N的值是相同的。
'示例:对于3x3矩阵,N为3。
'I As Byte:
'含义:I用作矩阵行的索引,通常从1开始,到N结束。
'示例:对于3x3矩阵,I的取值为1, 2, 3。
'I0 As Byte:
'含义:I0是一个辅助变量,用于计算当前行之前所有行的元素总数。它首先通过I - 1得到当前行的相对位置(从0开始计数),
'然后乘以N(矩阵的列数/大小)来得到之前所有行的元素总数。
'示例:对于3x3矩阵,当I=1时,I0=0;当I=2时,I0=3(因为第一行有3个元素);当I=3时,I0=6(因为前两行共有6个元素)。
'J As Byte:
'含义:J用作矩阵列的索引,通常从1开始,到N结束。
'示例:对于3x3矩阵,当I=2(即处理第二行)时,J的取值为1, 2, 3。
'Ij As Byte:
'含义:Ij是一个辅助变量,用于计算当前元素在一维数组中的索引位置。它通过I0 + J得到,
'其中I0表示当前元素之前所有元素的数量,J表示当前元素在当前行中的位置。
'示例:对于3x3矩阵,当I=2(第二行)且J=1时,Ij=I0+J=3+1=4,表示第二行第一个元素在一维数组中的索引为4。
'这段代码的目的是遍历一个NxN矩阵的所有元素,并通过计算每个元素在一维数组中的索引位置,以便
'可以对这些元素进行操作(如读取、修改等)。这种方法在处理需要将二维数组(如矩阵)转换为一维数组进行处理的场景时非常有用。
'////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
'请保持这种“直观”的变量表示法,如Ij、Ji、Ik等,因为当N=10、I=6、J=3时,I0=50。很容易看出Ij=I0+j,因为53=50+3。
'下面的示例和子程序可以在模拟器中运行。我没有配置串行输出,因此您无法直接看到输出结果。
'祝您在矩阵运算中玩得开心!
'作者:纳塔利乌斯
$regfile = "m328pdef.dat"
$crystal = 8000000
$baud = 19200
Const Nbyc = 4
Const Mbyc = 16 'Nbyc * Nbyc
Declare Sub Matadd()
Declare Sub Matsub()
Declare Sub Matmul()
Declare Sub Matinv()
Declare Sub Matprint(byval Ksi As Single)
Dim Iby As Byte , I0by As Byte , Ijby As Byte , Ikby As Byte , Irby As Byte
Dim Jby As Byte , J0by As Byte
Dim Kby As Byte , K0by As Byte , Kjby As Byte
Dim Rby As Byte , R0by As Byte , Riby As Byte , Rjby As Byte , Rrby As Byte , Rsby As Byte
Dim Sby As Byte , S0by As Byte , Siby As Byte , Srby As Byte , Ssby As Byte
Dim Iin As Integer
Dim Isi As Single , Jsi As Single , Ksi As Single , Msi As Single
Dim A(mbyc) As Single , B(mbyc) As Single , C(mbyc) As Single
'Temporary:
Dim M1(mbyc) As Single , M2(mbyc) As Single , M3(mbyc) As Single , M4(mbyc) As Single , M5(mbyc ) As Single
'用(伪)随机数填充矩阵A
'
For Iby = 1 To Mbyc
Iin = Rnd(1000)
Isi = Iin
A(iby) = Isi / 100
Next Iby
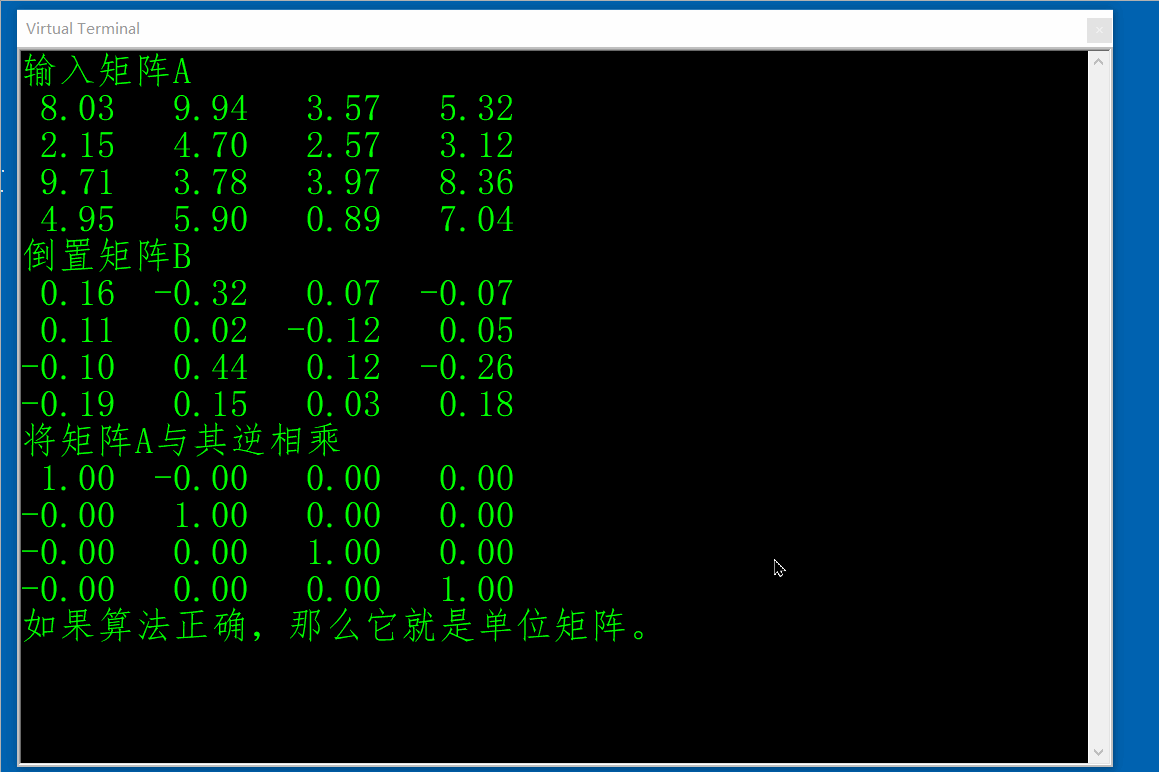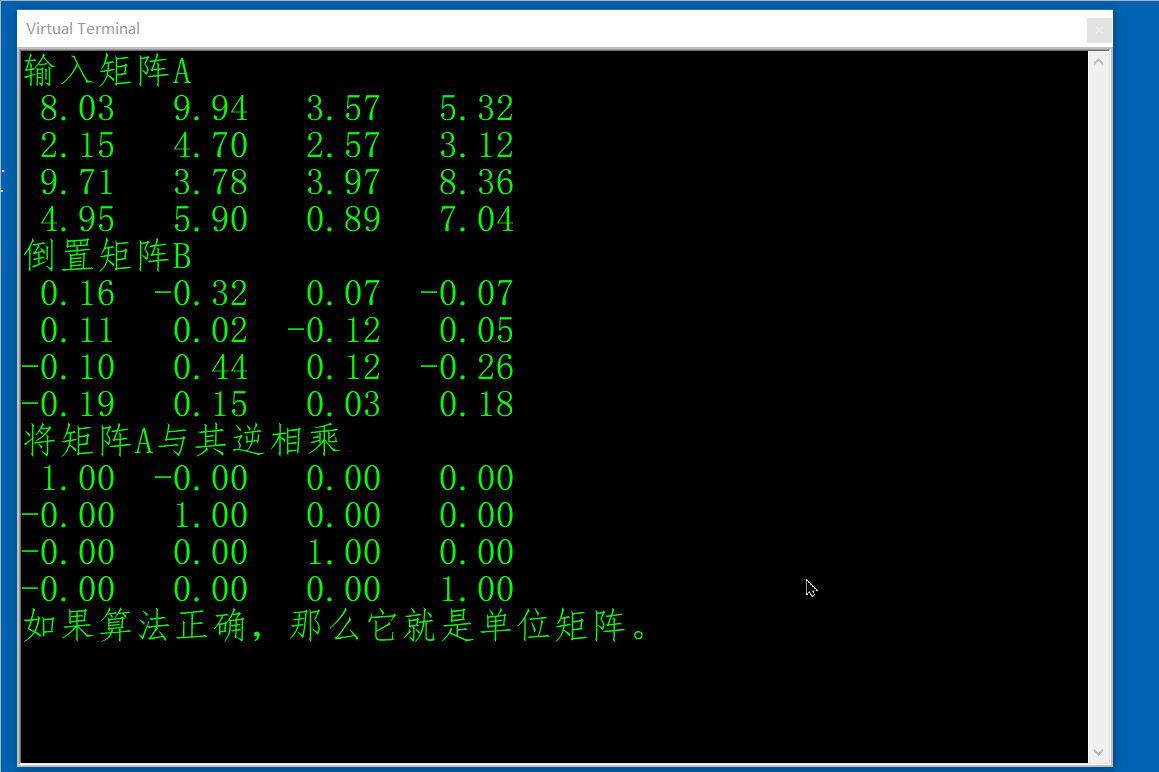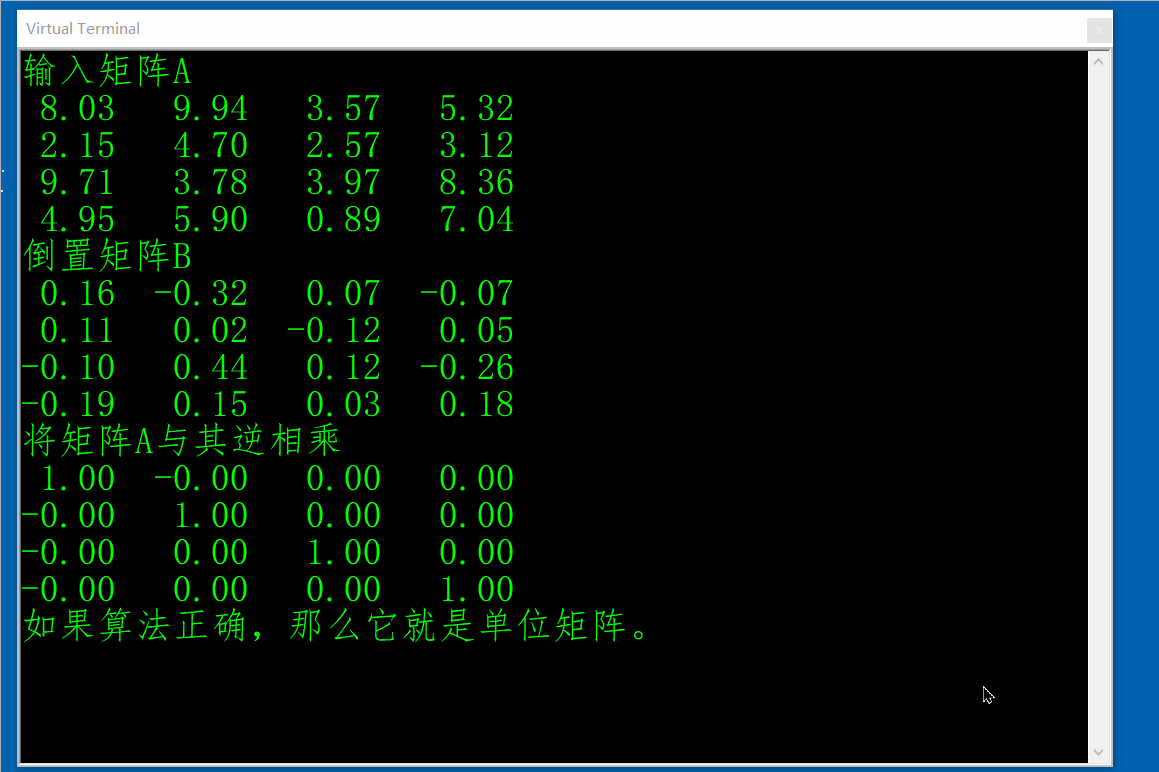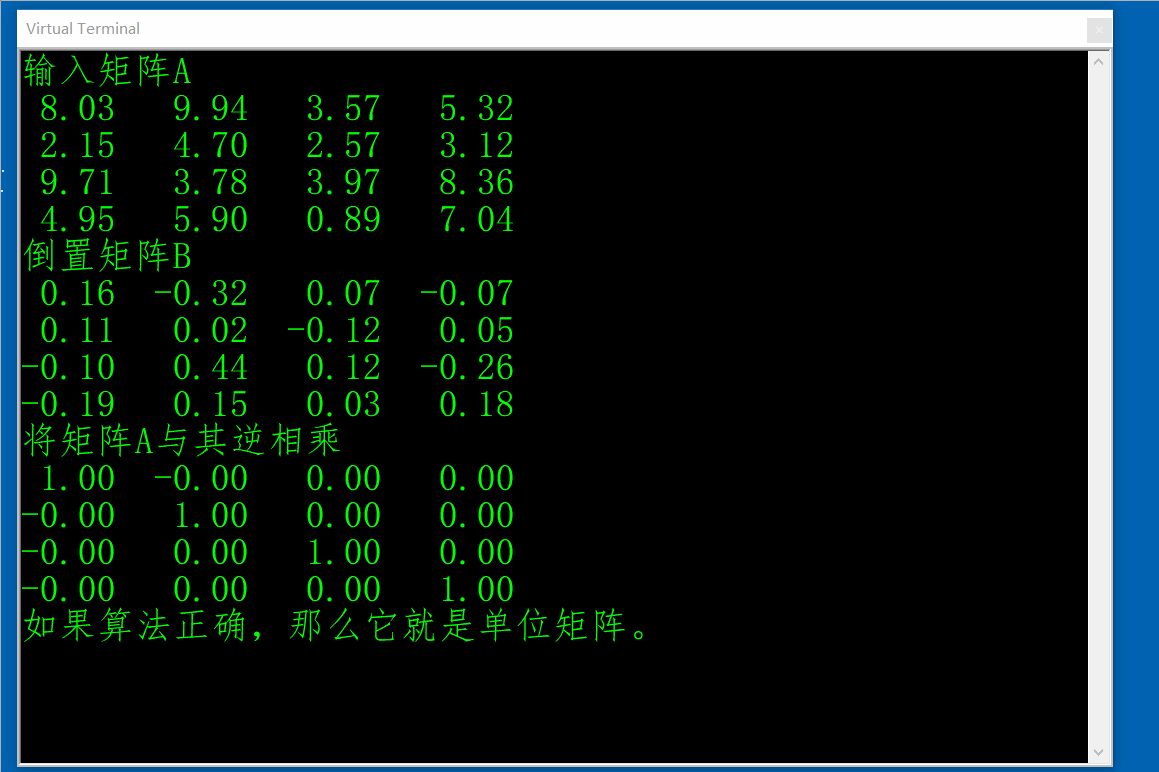
Print "输入矩阵A"
Matprint A(1)
Matinv
Print "倒置矩阵B"
Matprint B(1)
Matmul
Print "将矩阵A与其逆相乘"
Matprint C(1)
Print "如果算法是正确,那么它就是单位矩阵。"
'请注意,当从矩阵及其逆矩阵重新建立单位矩阵时,浮点运算的有限精度永远不会导致真正的零出现。
'零会表现为极小的正数或负数。这就是为什么打印出的是-0.00和0.00的原因。
End 'end program
'*******************************************************************************
'******************************* 矩阵加法 *******************************
'*******************************************************************************
Sub Matadd 'C = A + B
For Iby = 1 To Mbyc
C(iby) = A(iby) + B(iby)
Next Iby
End Sub
'*******************************************************************************
'******************************* 矩阵减法 ****************************
'*******************************************************************************
Sub Matsub 'C = A - B
For Iby = 1 To Mbyc
C(iby) = A(iby) - B(iby)
Next Iby
End Sub
'*******************************************************************************
'*************************** 矩阵乘法*****************************
'*******************************************************************************
Sub Matmul 'C = A * B
For Iby = 1 To Nbyc
I0by = Iby - 1
I0by = I0by * Nbyc
For Jby = 1 To Nbyc
Ijby = I0by + Jby
C(ijby) = 0
For Kby = 1 To Nbyc
K0by = Kby - 1
K0by = K0by * Nbyc
Kjby = K0by + Jby
Ikby = I0by + Kby
Jsi = A(ikby) * B(kjby)
C(ijby) = C(ijby) + Jsi
Next Kby
Next Jby
Next Iby
End Sub
'*******************************************************************************
'******************************* 矩阵求逆 ******************************
'*******************************************************************************
Sub Matinv 'B = 1/A
'
'将原始矩阵A复制到M1中
'
For Iby = 1 To Mbyc
M1(iby) = A(iby)
Next Iby
'
'填充两个单位矩阵:对于i等于j的情况,M2(i,j) = 1,M4(i,j) = 1;
'对于i不等于j的情况,M2(i,j) = 0,M4(i,j) = 0。
For Iby = 1 To Nbyc
I0by = Iby - 1
I0by = I0by * Nbyc
For Jby = 1 To Nbyc
Ijby = I0by + Jby
If Iby = Jby Then
M2(ijby) = 1
M4(ijby) = 1
Else
M2(ijby) = 0
M4(ijby) = 0
End If
Next Jby
Next Iby
For Rby = 1 To Nbyc 'Row byte RBy
R0by = Rby - 1 '0, 1, 2, 3..
R0by = R0by * Nbyc '0,Nbyc,2Nbyc,3Nbyc
Isi = 0
'------------------------------------'Pivotation中心点或轴
For Iby = Rby To Nbyc '矩阵或表格的对角线开始提取或构建行
I0by = Iby - 1
I0by = I0by * Nbyc
Irby = I0by + Rby 'index of element in 1D: Ir一维中元素的索引
Jsi = M1(irby)
Jsi = Abs(jsi)
If Jsi >= Isi Then '找到最大的元素
Isi = Jsi '
Sby = Iby '记住用于交换行的(操作或步骤)
End If
Next Iby
S0by = Sby - 1
S0by = S0by * Nbyc
For Iby = 1 To Nbyc
Riby = R0by + Iby 'Row R , column I “R”代表行号,而“I”代表列号。
Siby = S0by + Iby 'Row to swap, “要交换的行”
Swap M1(riby) , M1(siby)
Next Iby
Rrby = R0by + Rby
Jsi = M1(rrby)
Jsi = Abs(jsi)
If Jsi < 10e-30 Then
Print "奇异矩阵:无法进行求逆"
End If
'End Sub
Ssby = S0by + Sby
Rsby = R0by + Sby
Srby = S0by + Rby
M4(rrby) = 0
M4(ssby) = 0
M4(rsby) = 1
M4(srby) = 1
'-----------------------------------' 高斯-约旦消元法(Gauss-Jordan Elimination)
For Iby = 1 To Nbyc
I0by = Iby - 1
I0by = I0by * Nbyc
Irby = I0by + Rby
For Jby = 1 To Nbyc
J0by = Iby - 1
J0by = J0by * Nbyc
Ijby = I0by + Jby
Rjby = R0by + Jby
If Iby = Rby Then
If Iby = Jby Then
M3(rrby) = 1 / M1(rrby)
Else
M3(ijby) = M1(ijby) / M1(rrby)
M3(ijby) = 0 - M3(ijby)
End If
Elseif Jby = Rby Then
M3(irby) = M1(irby) / M1(rrby)
Else
Jsi = M1(rjby) * M1(irby)
Jsi = Jsi / M1(rrby)
M3(ijby) = M1(ijby) - Jsi
End If
Next Jby
Next Iby
'-----------------------------' 矩阵乘法 M5 = M4 × M2
For Iby = 1 To Nbyc
I0by = Iby - 1
I0by = I0by * Nbyc
For Jby = 1 To Nbyc
Ijby = I0by + Jby
M5(ijby) = 0
For Kby = 1 To Nbyc
K0by = Kby - 1
K0by = K0by * Nbyc
Kjby = K0by + Jby
Ikby = I0by + Kby
Jsi = M4(ikby) * M2(kjby)
M5(ijby) = M5(ijby) + Jsi
Next Kby
Next Jby
Next Iby
'---------------------------' 用M3,M5覆盖矩阵M1,M2
For Iby = 1 To Nbyc
I0by = Iby - 1
I0by = I0by * Nbyc
For Jby = 1 To Nbyc
Ijby = I0by + Jby
M2(ijby) = M5(ijby)
M1(ijby) = M3(ijby)
If Iby = Jby Then ' 重建单位矩阵 M4
M4(ijby) = 1
Else
M4(ijby) = 0
End If
Next Jby
Next Iby
Next Rby
'-------------------------------' 矩阵乘法 B = M1×M2
For Iby = 1 To Nbyc
I0by = Iby - 1
I0by = I0by * Nbyc
For Jby = 1 To Nbyc
J0by = Jby - 1
J0by = J0by * Nbyc
Ijby = I0by + Jby
B(ijby) = 0
For Kby = 1 To Nbyc
K0by = Kby - 1
K0by = K0by * Nbyc
Ikby = I0by + Kby
Kjby = K0by + Jby
Jsi = M1(ikby) * M2(kjby)
B(ijby) = B(ijby) + Jsi
Next Kby
Next Jby
Next Iby
End Sub
'*******************************************************************************
'******************************* 打印矩阵 **************************************
'*******************************************************************************
Sub Matprint(byval Ksi As Single)
Jby = 0 : Kby = 0
If Ksi = A(1) Then
Kby = 1
Elseif Ksi = B(1) Then
Kby = 2
Elseif Ksi = C(1) Then
Kby = 3
End If
For Iby = 1 To Mbyc
Select Case Kby
Case 1
Msi = A(iby)
Case 2
Msi = B(iby)
Case 3
Msi = C(iby)
Case Else
Exit Sub
End Select
If Msi >= 0 Then
Print " ";
End If
Print Fusing(msi , "#.##") ; " ";
Incr Jby
If Jby = Nbyc Then
Print
Jby = 0
End If
Next Iby
End Sub
Proteus 仿真输出结果:
|