在日常生活中,我们一直在做着“模式识别”。例如,迎面走来一个人,我们可以很快的判断出,这是“女”的或者是“男”的。这通常是通过人类的性别特征((De)Merkmal,(Eng)feature)做出这样判断的。例如是否有喉结和胡须,胸部是否突出等。
对于人类来说,这样的“模式识别”(分类判断)再简单不过了,可是这却是大脑高级功能的具体体现。要让计算机也能做到这一点,就非常不容易了。
而模式识别这门学科就是研究如何让计算机自动根据从环境中所检测到的信号对客体做出某种判断。(注:客体,为被进行分类的物体。)“基于统计”的意思是,进行判断的原理是基于概率统计学的。例如,当迎面走过来的人,既有胡须,胸部又突出时,按照模型判断其是女人的概率为0.75,是男人的概率为0.25,则判断结果了,此人是“女”的。
现在按照学习的讲义,一章章的进行复习,并整理其重点。Inhalt (课程内容)
?? Einführung (导论)
?? Elemente der Wahrscheinlichkeitsrechnung (概率原理)
?? Bayes’sche Entscheidungstheorie (贝叶斯判定理论)
?? Parametersch??tzung (参数估计)
?? Nichtparametrische Dichtesch??tzung und Klassifikation (非参数的密度估计和分类)
?? Lineare Methoden der Merkmalsreduktion (削减特征的线性方法)
?? Lineare Klassifikatoren (线性分类)
?? Expectation Maximization und das Lernen von Mischverteilungen (期望最大化和混合分布的学习)
?? Support Vector Machines (支持向量机)
?? Modell-Auswahl und Bewertung (模型的选择和评估)
第一章,导论。最典型的模式识别是如何进行的呢?
以如何判断男女的为例说明,
1,设置摄像头,拍摄照片
2,照片的前期处理,例如去除背景噪音,将照片中的人相部分切割出来等。
3,提取出特征:1)高度 2)亮度 等
4,根据所提取出的特征值,使用分类器进行分类。
(注,为什么在这里不用之前提到的喉结等特征呢? 这是因为喉结本身即是一个很高级的概念了。一张黑白照片可以理解为一个矩阵。每个像素的灰度值即为矩阵的各个值。所以最基本的特征值为,像素的灰度值。所有的信息都是从这个矩阵中提取出来的。例如高度可以定义为被占用的像素在纵向方向上的最大距离差。)
下面一个实际的例子进一步说明。
如图1所示,为大马哈鱼和鲈鱼的特征值比较(在此例中特征值为同一照明环境中的光亮程度)
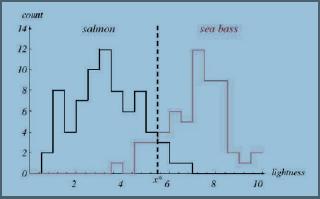
图1
图1说明:横轴为鱼的亮度,纵轴为鱼的数量。黑色和红色的直方图为根据实验得到的关于亮度的分布直方图。黑色的为大马哈鱼的,红色的为鲈鱼的。可以看出,总体上来说,鲈鱼的亮度要比大马哈鱼的要高。
从图中很明显的可以看出,在图中虚线的左边部分,大马哈鱼的概率要高于鲈鱼(黑色曲线在红色曲线上方),而到了虚线右边则鲈鱼的概率要高于大马哈鱼。
我们取图中虚线为亮度的阀值作为判定标准。(即,大于该阀值的判定为鲈鱼,否则为大马哈鱼。)
这个例子说明了如何进行的最基本的理念,即,概率大者胜。而整个模式识别就是研究如何建立一个高效的,错误少的判定模型。这将在之后的几章逐步介绍。
第二章,概率原理
前面说了,模式识别的基本理念是“概率大者胜”,那么在开始之前,进行一些概率原理的介绍是必要的。有兴趣的可以简单看一下。
2.1最重要的一些概念,包括:
1,条件概率(Bedingte Wahrscheinlichkeiten)
P(B|A),即当A发生时,B发生的概率。
2,联合概率(Verbundwahrscheinlichkeiten)
P(A,B),即A和B同时发生时的概率。
P(A,B) = P(B|A)P(A) = P(A|B)P(B)
当A和B统计无关时P(A,B) = P(A)P(B)
3,贝叶斯定理(Das Bayes-Theorem)
P(B|A) = P(A|B)P(B)/P(A)
2.2 离散随机变量
概率函数(Die Wahrscheinlichkeitsfunktion)
期望 μ或E[x](Erwartungswerte)
方差 σ^2或Var[x](die Varianz)Var[x] = σ^2 = E[(x ?? μ)^2]
成对的离散随机变量(Paare diskreter Zufallsvariablen)pij = Pr(x = vi, y = wj) ,用于有多个特征时。
协方差(Die Kovarianz)σxy = E[(x ?? μx)(y ?? μy)],用于描述变量x和y的概率相关性。当它们无关时等于0.
随机向量(Zufallsvektoren)x = [x1, x2, . . . , xd]T 注:T表示转置矩阵
P(x1, x2, x3, x4, x5) = P(x1, x2, x3, x4|x5)P(x5)
= P(x1, x2, x3|x4, x5)P(x4|x5)P(x5)
= ...
2.3连续随机变量
分布密度(Die Verteilungsdichte),对连续的随机变量来说,其概率大小已经没有意义了。因为其总是无限趋近于0。所以我们使用分布密度来表示概率大小。密度越大,概率越大,在某个区间内的概率为分布密度在该区间内的积分(当取值为从负无穷大到α时,即为分布函数(Die Verteilungsfunktion)F(α))。
2.4正态分布(Normalverteilung)
有兴趣的就看百度里的解释吧。(其实更喜欢wiki,不过好像国内有的时候打不开)
2.5马氏距离(Mahalanobis-Abstand)
欧氏距离和马氏距离
2.6 相关联随机变量的多变量正态分布
还有很多进一步的说明和概念,因本文主要是为了自己复习整理重点,所以在此就不一一细说了。
*第三章:Bayes’sche Entscheidungstheorie (贝叶斯判定理论)
回顾之前的将鱼进行分类的例子。我们可以用一种最直接的判断方法,即,此次捕捞中,哪种鱼的概率大就判断所有的鱼为该种鱼。很明显这样的判断方法太过于简单。因为被捕捞的概率和鱼本身没有很直接的关联。更好的方法就是,选取和鱼的种类直接相关的物理特征值,例如长度,重量,亮度等等,作为判定的依据。
以亮度为例:
如果 P(ω1|x) > P(ω2|x) → 判定为ω1
如果 P(ω1|x) < P(ω2|x) → 判定为ω2
其中,ω1,ω2为种类,P(ω1|x)为亮度为x时,ω1的分布密度。
这样的分类称为最大后验概率规则(Maximum-a-posteriori-Regel(MAP))。
由贝叶斯定理我们知道
P(ωj|x) = p(x|ωj) · P(ωj)/p(x)
其中,P(ωj|x)为后验概率,即;p(x|ωj) 为似然(即,可能性);P(ωj)为先验概率;而p(x)与模式识别没有什么关系。
上述概念在百度百科中的注解为:
1,先验概率是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现。在这里是此次捕捞中,两种鱼所占的比例。先验概率通常是根据历史资料进行的猜测。
"的信息后洲正的概率,如贝叶私中的,是"执果寻因"问题中的"因"。因为,是根据先验概率求出来的,所以称为后验概率。
当无法猜测出各种鱼的比例时,则可以采用最大似然判定规则(Maximum-Likelihood-Regel(ML))
如果p(x|ω1) > p(x|ω2) → 判定为ω1
如果p(x|ω2) > p(x|ω1) → 判定为ω2
错误概率的计算(Berechnung der Fehlerwahrscheinlichkeit)
很显然上面的判定规则都有误判的情况出现,那么错误的概率又是多大呢?我们如何才能降低出错的概率呢?
以只有两个种类的分类问题为例子说明。
对于只有两类的分类问题来说,误判指的是以下2种情况:
1,α2|ω1; 即 x ∈ R2|ω1,也就是说,本来是ω1,但是判定为ω2;
2,α1|ω2; 即 x ∈ R1|ω2,也就是说,本来是ω2,但是判定为ω1。
而总的误判概率则为:
P(error) = P(x ∈ R2, ω1) + P(x ∈ R1, ω2)
用图可以很直观的理解上面的概念。
如图2所示,为根据MAP规则进行分类的图。
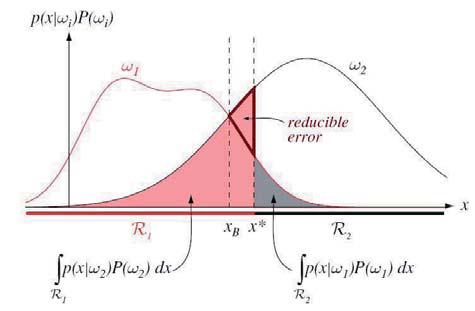
图2说明,横轴为特征值x,纵轴为后验概率。红色曲线为ω1的分布密度函数,黑色曲线为ω2的分布密度函数。红色和灰色区域为误判的情况,其面积为误判概率。
随着虚线(判定阀值)从右向左移动,错判的概率在减小(红色的粗框三角形区域为减少的部分)。
至此,贝叶斯判定理论算是基本介绍完了。当然,这只是最简单的例子,在实际应用中会比这个复杂的多。
第三章中进一步重要的内容还有:
Diskriminanzfunktionen (第四次习题内容)
Klassifikation auf der Basis von Gruppen benachbarter Pixel (第五次习题内容)
Neyman-Pearson-Test (第四次习题内容)
第四章,参数估计(待续)
第五章,期望最大化和混合分布的学习(待续)
第六章,非参数的密度估计和分类(待续)
第七章,线性分类(待续)
第八章,支持向量机(待续)
第九章,削减特征的线性方法(待续)
注:本文的德语讲义部分均摘自吕贝克大学ISIP学院A. Mertins教授的Stat. Mustererkennung的讲义中。如有转载,请注明来源。
|