钟表问题 一题多解锻炼数学的思维

若当前时刻为12点整，则时针和分针均指向刻度12。随后，因为两者的角速度不同，因此逐渐分开，但经过1小时后，分针转过一周，有赶上时针的趋势，因此两者渐渐重合。1点整时，分针指向刻度12，时针指向刻度1；1点5分时，分针恰指向刻度1，时针则超过刻度1。由于表盘上共有12大格（介于刻度1，2，3…，12之间），每个大格又被分为5小格，则时针前进1大格为1小时，前进1小格为12分钟。由此可以看出，1点5分时，时针位于刻度1后第1小格的5/12处；而在1点零6分时，分针恰指向刻度1后第1小格处，时针介于第1小格的6/12=1/2处。因此，1点零5分时，时针在分钟之前；1点零6分时，分针已超过时针。两者重合发生在这两个时刻之间。

算术求解：其实该钟表问题类似于算术中的“追击”问题。只要选择好运动的起点，便可以套用公式：追击时间=路程/速度差求解。分针的角速度为1（小格/分钟），时针的角速度为其1/12（小格/分钟）。两者速度差为11/12（小格/分钟）。我们选择运动起点为1点整，此时分针落后时针5小格，因此：

即两者重合时间为1点5分27.3秒。

       代数求解：分针角速度为时针角速度的12倍，因此若设时针从1点整起到两针重合时走过的角度为x（单位：小格），则分针走过的距离为12x；另外，注意到1点整时，分针指向刻度12，时针指向刻度1，两者相差5小格。建立方程如下：

则

分针走过了5.45小格，结果同算术求解。

       等比数列公式求解：高等数学求解的思考过程是在初始条件下，考虑分针追击时针的过程。1点整时，时针（处于刻度1处）超前分针（处于刻度12处）5小格；则5分钟后分针到达刻度1，时针前进了5/12小格；下一次追击，分针前进5/12小格，时针前进（5/12）/12小格；如此下去，则两者最终相差为无穷小量，即分针追上时针。在此过程中，分针走过距离为：

答案同算术、代数解法。

分析求解：最开始我们已分析出12点整后，分针、时针将于1点5分后1点6分之间相遇，但我们尚不知准确的时刻。继续按照这个思路分析，则在2点整后，两者相遇发生2点10分之后；3点整后，两者相遇发生3点15分之后；4点整后，两者相遇发生4点20分之后……两者12小时内最后一次重合发生在下一个12点整，其间共发生12次重合。又因为时针、分针都是匀速转动，因此每次重合间时间段相等。这也就是说，每次间隔为12/11大格（代表小时），或者60/11小格(代表分钟)。依次重合的时间为：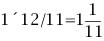

小时，而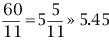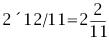

小时，而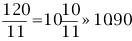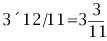

小时，而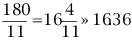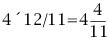

小时，而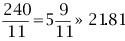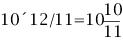

………

小时，而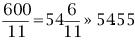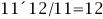

小时。

由此我们得到了12小时内每次时针、分针重合的时刻。

       由上面四种可以看出不同解法的思维特点。对问题进行正确的分析时各种解法的基础，但是算术解法和代数解法侧重点在于确立一个初始状态和终了状态，并通过两者的等值关系求解。而高等数学方法则是将上述追击过程直接通过一个无穷级数计算，并根据级数的收敛性得出结果。因此，虽然计算过程看似复杂，然而思考的过程确简单明了。分析求解方法则是分析了时针、分针重合的特点，通盘考虑求解，也具有鲜明的特点。