|
|
心形线(Cardioid)
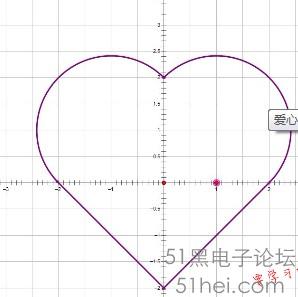
直角坐标方程:(x^2+y^2-2*a*x)^2=4*a^2*(x^2+y^2)
极坐标方程:r=2*a*(1+cos(theta))
参数方程:x=a*(2*cos(t)-cos(2*t)),y=a*(2*sin(t)-sin(2*t))
玫瑰曲线
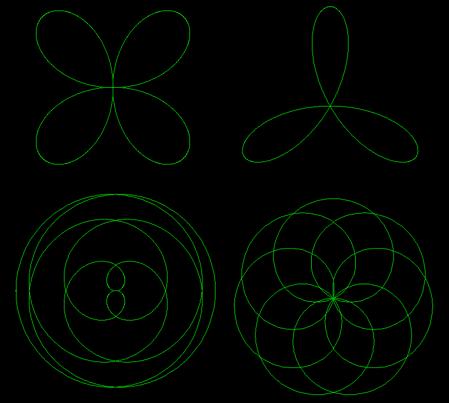
参数方程 :x = r * sin(k * t) * cos(n* t)); y = r * sin(k * t) * sin(n* t); 0<=t<=2*PI
极坐标方程:ρ=rsin(nt) ;
如果k是整数,当k是奇数时那么曲线将会是k个花瓣,当k是偶数时曲线将是2k个花瓣。如果k为非整数,将产生圆盘(disc)状图形,且花瓣数也为非整数。注意:该方程不可能产生4的倍数加2(如2,6,10……)个花瓣。变量r代表玫瑰线花瓣的长度。
椭圆方程:
当焦点在x轴时,椭圆的标准方程是:x^2/a^2+y^2/b^2=1,(a>b>0);
当焦点在y轴时,椭圆的标准方程是:y^2/a^2+x^2/b^2=1,(a>b>0);
其中a^2-c^2=b^2
椭圆的参数方程x=acosθ,y=bsinθ,0<=θ<=2*PI
双曲线:
参数方程:x=x0+asecθ,y=y0+btanθ ;
(x0,y0)为中心,a为实轴长,b为虚半轴长,θ为离心角
直角坐标系:(x-x0)^2/a^2-(y-y0)^2/b^2=1
阿基米德螺旋线的标准极坐标方程
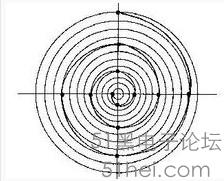
r(θ)= a+ b(θ)
式中:
b—阿基米德螺旋线系数,mm/°,表示每旋转1度时极径的增加(或减小)量;
θ—极角,单位为度,表示阿基米德螺旋线转过的总度数;
a—当θ=0°时的极径,mm。
改变参数a将改变螺线形状,b控制螺线间距离,通常其为常量。阿基米德螺线有两条螺线,一条θ>0,另一条θ<0。两条螺线在极点处平滑地连接。把其中一条翻转 90°/270°得到其镜像,就是另一条螺线。
星形线:
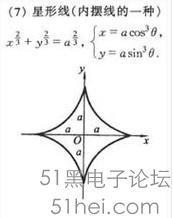
直角坐标方程:x^(2/3)+y^(2/3)=a^(2/3)
参数方程:x=a*(cost)^3,y=a*(sint)^3 (t为参数)
伯努利双纽线
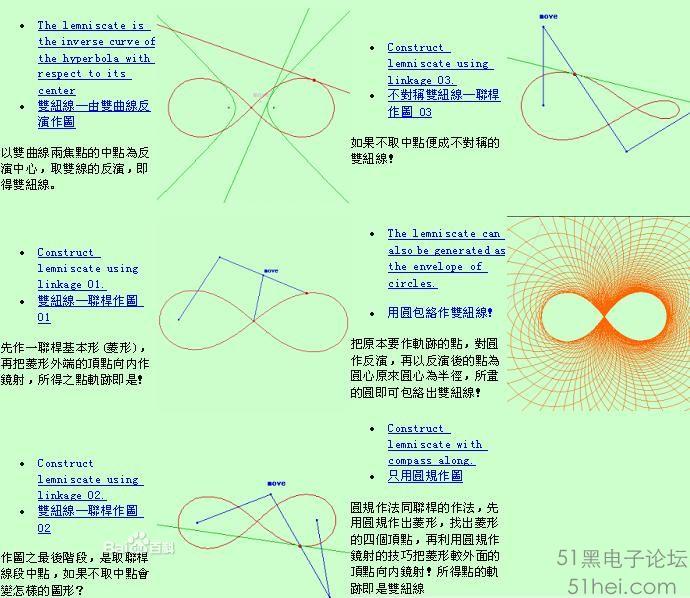
直角坐标系:(x + y) = 2a(x − y) ρ^2=a^2·sin2θ (左图)
和ρ^2=a^2·cos2θ (右图)
梅花曲线
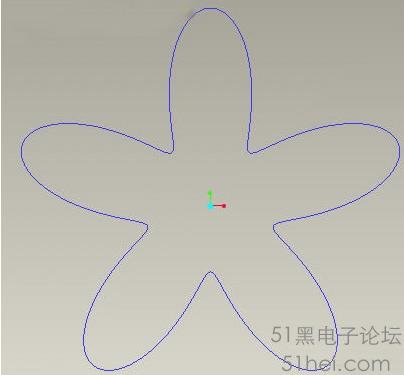
r=100+50*cos(5* θ ) 0<=θ<=2*PI
z=2*cos(5* θ )
|
|