矩阵相乘问题描述:给定n个矩阵{A1,A2,...,An},当然A1到An的任意段都是可乘的,求最小相乘次数。例如有三个矩阵维数分别
为:10*100,100*2,2*5;若前两个相乘,再乘第三个,总的相乘次数=10*100*2+10*2*5=2100;若第二个与第三个先相乘,
在乘第一个,总相乘次数=100*2*5+10*100*5=5100;显然,相乘次序会对计算量有很大影响,如果你在学线性代数的时候,写了一个矩阵相
乘的程序,结果跑到同学那里演示的时候,半天没运行出来,那就尴尬了!!!
函数调用一般会要传参,这些参数都是非常有意义。这个题目属于动态规划,最重要的一点就是想到一个二维数组m[i][j],代表矩阵i到矩阵j相乘的最优
解,然后就是怎样给这个有意义的数组置数了,这种数组定义和数组置数若成,则我们要的答案就在m[1][n]中,代表矩阵1到矩阵n相乘的最优解。(如果
你很饥渴的想解决这个问题,就直接看代码吧!!)有人可能会问,为什么会想到这种数组定义,主要有两个方面:一,学习(高效),看多了自然会想到给数组某
种意义,培育一种思想;二、思考与分析,来的缓慢,但是凌驾与学习之上,也是学习的目的,是终极武器,也是基础武器。。。。
不扯了,回到主题,很明显如果只有一个矩阵,相乘次数为零;如果有两个,直接相乘,若第一个矩阵维数q*p,第二个矩阵维数p*r,相乘次数为
q*p*r;三个矩阵相乘,为前两相乘,再乘第三个,和后两个先相乘,再乘第一个,取其优者;四个矩阵相乘,设第三个矩阵维数r*t,第四个矩阵t*k,
维数min{前三个矩阵最优值+q*t*k,前两个矩阵最优+后两个矩阵最优+q*r*k,前一个矩阵最优+后三个矩阵最优+q*p*k};然后。。。
有人可能会问:我可以算出前一个,前两个,前三个矩阵相乘的最优,但是我怎么算出后一个,后两个,后三个相乘的最优呢?
其
实这个问题又回到了原点,这就是动态规划的妙处,显然我们先求出A1到An的任意段长度为2矩阵的最优(直接相乘),然后可以计算出任意段长度为3矩阵的
最优;然后。。。然后我们就想了个m[i][j]出来,记录我们求的的结果;然后再写代码,尝试思想的准确性,当然我们更多的时候是站在先人的肩膀上做验
证工作。。。
代码如下(参考教科书):
#include<iostream>
using namespace std;
void chain(int *p,int n,int m[][7],int s[][7])//p维数数组,m最优乘次数组,s记录划分方案
{
int j;
for(int i=1;i<=n;i++)
m[i][i]=0;
for(int r=2;r<=n;r++)
{
for(i=1;i<=n-r+1;i++)
{
j=i+r-1;
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i;
for(int k=i+1;k<j;k++)
{
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;
}
}
}
}
for(i=1;i<=n;i++) //我把它翻过来输出。。。
{
for(j=n;j>=i;j--)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
}
void Traceback(int i,int j,int s[][7]) //输出相乘方案
{
if(i==j)
return;
Traceback(i,s[i][j],s);
Traceback(s[i][j]+1,j,s);
cout<<"Multiply A "<<i<<","<<s[i][j];
cout<<" and B "<<(s[i][j]+1)<<","<<j<<endl;
return;
}
int main()
{
int p[7],m[7][7],s[7][7],n;
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<=n;i++)
{
scanf("%d",&p[i]);
}
chain(p,n,m,s);
Traceback(1,6,s);
}
return 0;
}
/*
p52
测试数据:
6
30 35 15 5 10 20 25
*/
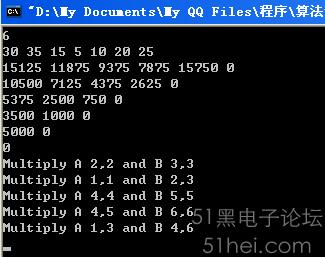
运行结果:
 |