学习递归是很神奇的。。
【前言】首先我得告诉你,这篇文章中充满了递归。如果你还不清楚递归,那么就准备进入逻辑的疯狂吧。
【故事2则】
1.【从前有座山】(递归短文)
从前有座山.山里有座庙.庙里有个老和尚和小和尚. 老和尚对小和尚说:“从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:"从前有座山.山里有座庙. 庙里有个老和尚和小和尚.老和尚对小和尚说:……""""""""""""""”
………………(如果你把上文一字不漏的看完了,你会堆栈溢出的。。)……………………
2.【生活中的递归】
假设你正在看新闻联播正在播放胡总视察基层工作,突然插播一条来自美国的现场报道;这条插播还没完,又插播一条来自叙利亚的现场报道……然后回到美国的报道;美国报道结束后,胡总又出现在屏幕上。这样,在一个视频内中断主视频引用了另一个视频实际上也是递归。
从某种角度看,这个世界就是递归的,所以在你知道递归的那一天,你可以大声地说:“我发现世界的本质啦哈哈哈哈哈哈哈哈哈,这个世界的本质就是‘我发现世界的本质啦哈哈哈哈哈哈哈哈哈,这个世界的本质就是……’”
理解递归是一件很值得自豪的事,递归在很多方面都有应用,它不仅仅是一种优秀的算法,更是一种先进的思想,(类似于分治思想)即使你没有学编程也没有关系。如果你理解了它,至少证明你的智商不容怀疑。。
【关于头痛的递归】
【Google英文搜索递归:(冷笑话一个,初识递归从笑话开始。。)】
(注:"Did you mean:Recursion"的意思是:“你是不是在找:‘递归’”)
【“递归”告诉你:】如果你想理解递归,你就先要理解递归。(这句话只有你理解了递归之后你才能理解。。。)
递归做为一种算法在程序设计语言中广泛应用。是指函数/过程/子程序在运行过程中直接或间接调用自身而产生的重入现象。就好像是循环,但相对来说,比循环更难理解。
【递归经典例子:】
【阶乘】
在数学里,阶乘函数是这样定义的:
F(x)=1 (x=1时)
或 x*F(x-1) (x>1时)
解释:
任意一个大于0的自然数的阶乘结果为:
当这个自然数为1时,结果为1
当这个自然数大于1时,其结果为这个自然数 乘以 (这个自然数-1)的阶乘
【菲波拉契数列】
菲波拉契数列,又称黄金分割数列。
菲波拉契数列的规律是:列表中的任意一个数等于前面两个数之和。通常列表的第一项是1.
也就是说,菲波拉契数列是这个样子:
1、1、2、3、5、8、13、21、……
在数学中,菲波拉契数列被用递归定义:
Fib(n)=0 ,n=0
Fib(n)=1 ,n=1
Fib(n)=Fib(n-1)+Fib(n-2) ,n>1
也就是说,任意一个项可以这样求得:(n为项数。(n为自然数))
如果需要求的项数为0,那么结果为 0
如果需要求的项数为1,那么结果为 1如果需要求的项数>1,那么结果为 菲波拉契数列中的第n-1项 与 菲波拉契数列中的第n-2项 之和。
【练习】:
用上面的方法手动求菲波拉契数列的第3项,和3的阶乘。
【如果你弄懂了……】
如果你弄懂了而且还没学过编程,那么你是高智商无疑了。。自信的留言自豪一下吧。。
如果没有弄懂了递归,那么你需要弄懂递归。(或者说找另一个人来帮你理解一下这篇文章。。)
【传说中先进的递归思想!(建议你一定要看看)】
【汉诺塔(hanoi)】
汉诺塔:汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。
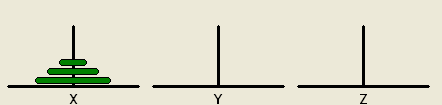
这个游戏的目标是,借助Y塔,将X塔上的所有盘子移到Z塔上。但一次只准移动一个盘子,而且只准把小盘子压在大盘子上,而不允许将大盘子压在小盘子上。
这看起来似乎很麻烦,难道不是吗?但实际上3个盘子还是很好办的,7步。(2个盘子最好办),但是汉诺塔有他的难度等级,有些疯子甚至喜欢玩11阶、甚至是16阶汉诺塔。
这听起来好像很简单,真的吗?以下是8阶汉诺塔的解法:(255步)
8阶汉诺塔解法0.
1.X ==> Y
2.X ==> Z
3.Y ==> Z
4.X ==> Y
5.Z ==> X
6.Z ==> Y
7.X ==> Y
8.X ==> Z
9.Y ==> Z
10.Y ==> X
11.Z ==> X
12.Y ==> Z
13.X ==> Y
14.X ==> Z
15.Y ==> Z
16.X ==> Y
17.Z ==> X
18.Z ==> Y
19.X ==> Y
20.Z ==> X
21.Y ==> Z
22.Y ==> X
23.Z ==> X
24.Z ==> Y
25.X ==> Y
26.X ==> Z
27.Y ==> Z
28.X ==> Y
29.Z ==> X
30.Z ==> Y
31.X ==> Y
32.X ==> Z
33.Y ==> Z
34.Y ==> X
35.Z ==> X
36.Y ==> Z
37.X ==> Y
38.X ==> Z
39.Y ==> Z
40.Y ==> X
41.Z ==> X
42.Z ==> Y
43.X ==> Y
44.Z ==> X
45.Y ==> Z
46.Y ==> X
47.Z ==> X
48.Y ==> Z
49.X ==> Y
50.X ==> Z
51.Y ==> Z
52.X ==> Y
53.Z ==> X
54.Z ==> Y
55.X ==> Y
56.X ==> Z
57.Y ==> Z
58.Y ==> X
59.Z ==> X
60.Y ==> Z
61.X ==> Y
62.X ==> Z
63.Y ==> Z
64.X ==> Y
65.Z ==> X
66.Z ==> Y
67.X ==> Y
68.Z ==> X
69.Y ==> Z
70.Y ==> X
71.Z ==> X
72.Z ==> Y
73.X ==> Y
74.X ==> Z
75.Y ==> Z
76.X ==> Y
77.Z ==> X
78.Z ==> Y
79.X ==> Y
80.Z ==> X
81.Y ==> Z
82.Y ==> X
83.Z ==> X
84.Y ==> Z
85.X ==> Y
86.X ==> Z
87.Y ==> Z
88.Y ==> X
89.Z ==> X
90.Z ==> Y
91.X ==> Y
92.Z ==> X
93.Y ==> Z
94.Y ==> X
95.Z ==> X
96.Z ==> Y
97.X ==> Y
98.X ==> Z
99.Y ==> Z
100.X ==> Y
101.Z ==> X
102.Z ==> Y
103.X ==> Y
104.X ==> Z
105.Y ==> Z
106.Y ==> X
107.Z ==> X
108.Y ==> Z
109.X ==> Y
110.X ==> Z
111.Y ==> Z
112.X ==> Y
113.Z ==> X
114.Z ==> Y
115.X ==> Y
116.Z ==> X
117.Y ==> Z
118.Y ==> X
119.Z ==> X
120.Z ==> Y
121.X ==> Y
122.X ==> Z
123.Y ==> Z
124.X ==> Y
125.Z ==> X
126.Z ==> Y
127.X ==> Y
128.X ==> Z
129.Y ==> Z
130.Y ==> X
131.Z ==> X
132.Y ==> Z
133.X ==> Y
134.X ==> Z
135.Y ==> Z
136.Y ==> X
137.Z ==> X
138.Z ==> Y
139.X ==> Y
140.Z ==> X
141.Y ==> Z
142.Y ==> X
143.Z ==> X
144.Y ==> Z
145.X ==> Y
146.X ==> Z
147.Y ==> Z
148.X ==> Y
149.Z ==> X
150.Z ==> Y
151.X ==> Y
152.X ==> Z
153.Y ==> Z
154.Y ==> X
155.Z ==> X
156.Y ==> Z
157.X ==> Y
158.X ==> Z
159.Y ==> Z
160.Y ==> X
161.Z ==> X
162.Z ==> Y
163.X ==> Y
164.Z ==> X
165.Y ==> Z
166.Y ==> X
167.Z ==> X
168.Z ==> Y
169.X ==> Y
170.X ==> Z
171.Y ==> Z
172.X ==> Y
173.Z ==> X
174.Z ==> Y
175.X ==> Y
176.Z ==> X
177.Y ==> Z
178.Y ==> X
179.Z ==> X
180.Y ==> Z
181.X ==> Y
182.X ==> Z
183.Y ==> Z
184.Y ==> X
185.Z ==> X
186.Z ==> Y
187.X ==> Y
188.Z ==> X
189.Y ==> Z
190.Y ==> X
191.Z ==> X
192.Y ==> Z
193.X ==> Y
194.X ==> Z
195.Y ==> Z
196.X ==> Y
197.Z ==> X
198.Z ==> Y
199.X ==> Y
200.X ==> Z
201.Y ==> Z
202.Y ==> X
203.Z ==> X
204.Y ==> Z
205.X ==> Y
206.X ==> Z
207.Y ==> Z
208.X ==> Y
209.Z ==> X
210.Z ==> Y
211.X ==> Y
212.Z ==> X
213.Y ==> Z
214.Y ==> X
215.Z ==> X
216.Z ==> Y
217.X ==> Y
218.X ==> Z
219.Y ==> Z
220.X ==> Y
221.Z ==> X
222.Z ==> Y
223.X ==> Y
224.X ==> Z
225.Y ==> Z
226.Y ==> X
227.Z ==> X
228.Y ==> Z
229.X ==> Y
230.X ==> Z
231.Y ==> Z
232.Y ==> X
233.Z ==> X
234.Z ==> Y
235.X ==> Y
236.Z ==> X
237.Y ==> Z
238.Y ==> X
239.Z ==> X
240.Y ==> Z
241.X ==> Y
242.X ==> Z
243.Y ==> Z
244.X ==> Y
245.Z ==> X
246.Z ==> Y
247.X ==> Y
248.X ==> Z
249.Y ==> Z
250.Y ==> X
251.Z ==> X
252.Y ==> Z
253.X ==> Y
254.X ==> Z
255.Y ==> Z
我相信没有哪个疯子会把上面的东东一字一句的看完
这很疯狂,不是吗?那回到正题,3阶汉诺塔又怎么个解法呢?
这就需要用我们神奇的递归思想了:
从前,有一个人叫A,他看到3阶汉诺塔毫无头绪。他有一堆帮手。
有一天这个A先生突发奇想,他想:我现在不知道3阶汉诺塔怎么移动到Z,但是要是有一个人帮我把X塔上的上面2个盘子移动到Y塔,我岂不是只需要移动最后一个盘子,然后再让他用同样的方法把Y塔上的2个盘子移动到Z上,问题不就解决了???
于是他命令B把2个盘子移动到Y上去……结果哪知道这B居然不知道怎么移。但他想:我现在不知道2阶汉诺塔怎么移动到Y,但是要是有一个人帮我把X塔上的上面1个盘子移动到Z塔,我岂不是只需要移动最后一个盘子,然后再让他用同样的方法把Z塔上的1个盘子移动到Y上?
……………………
……………………
于是问题就解决了!就像这样↓
3阶汉诺塔解法0.
1.X ==> Z
2.X ==> Y
3.Z ==> Y
4.X ==> Z
5.Y ==> X
6.Y ==> Z
7.X ==> Z
【我想,现在这些递归经典例子你应该能理解了……:】
【阶乘】
在数学里,阶乘函数是这样定义的:
F(x)=1 (x=1时)
或 x*F(x-1) (x>1时)
解释:
任意一个大于0的自然数的阶乘结果为:
当这个自然数为1时,结果为1
当这个自然数大于1时,其结果为这个自然数 乘以 (这个自然数-1)的阶乘
【菲波拉契数列】
菲波拉契数列,又称黄金分割数列。
菲波拉契数列的规律是:列表中的任意一个数等于前面两个数之和。通常列表的第一项是1.
也就是说,菲波拉契数列是这个样子:
1、1、2、3、5、8、13、21、……
在数学中,菲波拉契数列被用递归定义:
Fib(n)=0 ,n=0
Fib(n)=1 ,n=1
Fib(n)=Fib(n-1)+Fib(n-2) ,n>1
也就是说,任意一个项可以这样求得:(n为项数。(n为自然数))
如果需要求的项数为0,那么结果为 0
如果需要求的项数为1,那么结果为 1如果需要求的项数>1,那么结果为 菲波拉契数列中的第n-1项 与 菲波拉契数列中的第n-2项 之和。
【程序中的递归】
前面提到递归做为一种算法在程序设计语言中广泛应用。
是指函数/过程/子程序在运行过程中直接或间接调用自身而产生的重入现象。
那么,递归在程序中如何实现呢?
我们就以经典的“汉诺塔”为例,编写得这样一个程序:
#include <iostream.h>
#include <stdlib.h>
int n;
void mov(char a,char b);
//汉诺塔函数作用:递归主体部分。。
//参数解释:[n]:汉诺塔阶数。 [Start]:起始塔的名称。(如:X) [Temp]:临时塔的名称 [End]:目标塔的名称。
void hanoi(unsigned int n,char Start,char Temp,char End) {
if (n==1) { //如果只有一阶,
mov(Start,End); //那么直接将起始塔上的盘子移动到目标塔
} else if (n>=2) { //如果不止一阶 hanoi(n-1,Start,End,Temp);//(注意此处参数变化!)那么将除了最低端的盘子上面的所有盘子移动到临时塔
mov(Start,End); //移动最大的一个盘子(偷懒的过程在此)
hanoi(n-1,Temp,Start,End); //(注意此处参数变化!)用同样的方法将临时塔上的盘子移到目标塔上
}
}
void mov (char a,char b) { //mov函数作用:在屏幕上输出这一个步骤。(模拟移动的过程)
cout<<a;
cout<<">";
cout<<b;
cout<<endl;
system("pause");
}
void main (void) {
cout<<"请输入汉诺塔阶数:";
cin>>n;
cout<<"步骤如下:";
cout<<endl;
hanoi(n,'A','B','C');
cout<<"完成!";
cout<<endl;
system("pause");
}
程序很短,应该算是很易于理解吧。
【关于递归思想的冷笑话】
(如果你知道什么是递归了……那么看一个递归笑话吧……)
当你理解了递归后,你可以使用先进的递归思想解决实际问题:
我不知道什么是递归,我想要理解递归。要是有人帮我理解什么是“递归”那我岂不是不用理解了吗?于是找到另外一个人,要他理解一下递归。结果他也不知道什么是递归,他想要理解递归。要是有人帮他理解什么是“递归”那他岂不是不用理解了吗?于是他又找到另一个人,结果另一个人也不知道什么是递归,但那个人想,要是有人帮他理解什么是“递归”那他岂不是不用理解了吗?于是……最终结果是【栈溢出】!
您看懂了递归(指递归(指递归(指递归(指递归(指递归(指递归)))))))了吗?请提出您的建议!谢谢!
|