对于我等智力低下学历浅薄之徒,是无权谈论科学之数学的,只是有些事情总是萦绕在左右,不得释怀。就我所知的数学公式也不过是07年的滕老师版的简易概念性数学,至于初中和小学,我只能说我都藏猫猫了吧。滕老师版的数学也没学多少东西,等差数等比数列之流的通项试大概早已忘却了,抛物线和双曲线椭圆和圆。高等数学看了很久始终搞不明白积分和微分,函数还好些,毕竟还是写点程序的。复杂函数咱不会,线性函数总是会的吧。不过在某些控制理论上你是逃不开积分和微分的。最近对此又有了新的认识。记述一二,权且足迹了吧!
积分从面积开始,不论懂不懂什么是积分权且当做个概念吧,先从简单的入手,
假设:有一个坐标系 X,0,Y .x横坐标、y纵坐标,在Y=2点平行于X轴画一条直线,那么这条直线就是无论X在何地Y值总是2,显然X轴可以无限的长下去,再假设X=5;那么在(0,0)-(3,2)这个对角线做图围城一个矩形,那么矩形的面积S显然等于2*5=10;
但是这是我们所知道的计算面积的公式很简单,大家都知道,但是如果这个线是不规则呢?那又该怎么去计算线包围面积的呢?这时候就需要类似割圆术一类的极限逼近法啦,维基
在坐标系中的一条线可以用函数来描述,例如平方根函数y=根号下X的图像是一条不规则曲线,那么计算他的面积就要下图进行分割

表示为 这个S是面积, 这个S是面积, 这个玩意可以理解为SUM,也就是求和,就是西格玛的那个加法而已,这样就理解起来简单许多许多了,不用疑惑他是个啥玩意,dx这个必须要说一说,我被坑了很久,我以前一直不知道这个是个毛玩意,听别人说是分多少,这个其实是表示这个求和是在X轴刻度上进行的,如果把X轴换成T也就是时间,那就是以时间为粒度的积分,那才是研究积分的意义。到时候写进程序里的就是对T在时间轴上进行的积分。粒度就是采样率。采样率越高,越接近与真实就是这个道理。 这个玩意可以理解为SUM,也就是求和,就是西格玛的那个加法而已,这样就理解起来简单许多许多了,不用疑惑他是个啥玩意,dx这个必须要说一说,我被坑了很久,我以前一直不知道这个是个毛玩意,听别人说是分多少,这个其实是表示这个求和是在X轴刻度上进行的,如果把X轴换成T也就是时间,那就是以时间为粒度的积分,那才是研究积分的意义。到时候写进程序里的就是对T在时间轴上进行的积分。粒度就是采样率。采样率越高,越接近与真实就是这个道理。
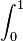 这个玩意是表示Y轴的值的范围,也就是积分域,这个对应程序里面的限幅滤波器,计算出来的值要在一定范围内变动,而不是任意的, 这个玩意是表示Y轴的值的范围,也就是积分域,这个对应程序里面的限幅滤波器,计算出来的值要在一定范围内变动,而不是任意的,
接下来就是求这线围成的面积,首先在函数线上找5个点然后向外做5各相邻的矩形,然后我们对5个矩形求和就是一个S1这个S1要比实际的面积S大,如下
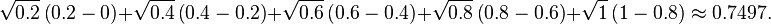
第二步继续分割,这次分割是向内做矩形,并且分的更细,X轴分为12,然后求和S2,S2一定比S小,如下:

由此可见S的真实面积就是 S2<S<S1
如果对X轴继续分下去,画出更多的矩形来,当点和点相邻时的小矩形面积之和就是S的面积,这就是积分
实际上是对不规则的形状用规则去丈量的思想,和割圆术一样的道理。
在程序中我面对的是以时间为X轴,温度差为Y轴的坐标系,我要知道误差的所有的采样点连成线的包围。那么采样率就是dt=MAX 0-760kHZ的倒数,程序中也没有积分,就是求和而已误差就是正MAX和负MAX,这个复杂一点,误差是在正负和0之间变化的,也就是定积分的积分域。可见假设采样率为实时的,那么就是真实的dt,可惜那是不可能的,最高采样也不用过800K,但是足以近似出来这个面积的真实大小。
老王于日照
|