链接已更换，可以下载了。
GraphicMathV1.4Beta.rar
(85.11 KB, 下载次数: 5)
更新日志：
2013-01-12
V1.0
1.实现了绘图和数值解方程。
2013-01-18
V1.1
1.加快了绘图速度，改进了绘图过慢的问题；
2.解决了解方程不正确的重大BUG
3.加入了导数图像绘制功能，使用方法：在函数前面添加 d/dx ,如 d/dx sin(x)
V1.2
2013-01-25
1.加入了极坐标
2.加入了参数方程
3.数值解微分方程功能（Euler折线法）
4.绘制斜率场功能
5.加入了坐标显示
6.加强了图形解方程功能，标出交点
V1.3
2013-02-03
1.增加了命令功能，目前支持8个基本命令：Plot Calc View Solve DSolve Cls RePlot Redo
2.改进了一些小问题
3.在Cyycoish的帮助下，改进了界面。感谢网友Cyycoish。
4.增加了二阶微分方程的功能（仍然Euler折线法，可能有一定误差，可视情况减小步长以减小误差）
5.改进了关于颜色的问题。
6.增加了保存图片功能。
7.增加了泰勒级数的计算。【注：目前算法不太完善，建议不要超过三阶，超过了三阶误差非常大。】
V1.4
1.使用RK4算法替代Euler折线法，精确度大大提高。
【快捷键】：
Ctrl+方向键移动视野
Ctrl+Del清屏
Ctrl+I放大
Ctrl+O缩小
Ctrl+A自动高度
Ctrl+N恢复默认视野
【命令及语法】：
目前有8个命令：Plot, Calc, View, Solve, DSolve, Cls, RePlot, Redo
语法帮助：输入 “命令 ?”（不含引号）然后回车即可询问语法。
Plot y1[; y2 ;y3; ...]
绘制函数图像。y1:函数解析式。用分号分隔。支持 y = 和 r = 。当没有指定 y或r时默认为 y =
Calc Expr
计算表达式。Expr:数值表达式。
View [XMin, XMax, YMin, YMax]
调整视野范围。不加参数则视为调整为初始大小。
Solve Equation [,X0]
数值解方程。Equation:方程式，未知数为x。X0:初始值，若没有指定则默认为1。
DSolve y'=... , X0, Y0 [, Step]
数值求解一阶微分方程。X0:初始x值。Y0:初始y值。Step:步长。若没有指定则默认0.001
DSolve y''=... , X0, Y0, YP0 [, Step]
数值求解二阶微分方程。X0:初始x值。Y0:初始y值。YP0:初始的y'的值。Step:步长。若没有指定则默认0.001
Cls
清除屏幕。
RePlot y1[; y2 ;y3; ...]
清屏后再绘制函数图像，语法与Plot相同
Redo [n]
执行前n次的命令。不指定n则默认n=1.n不可超过5.
新界面与新功能：
新版本风采
算法已经更新为RK4算法：
有图为证：
步长为0.01，y''+y=0 IVP{y(0)=1,y'(0)=0} 误差几乎没有（蓝色曲线是真实解）
相比V1.3版本：
（以下内容皆为V1.3版本）
sinx和sinx的导数：
支持多种坐标系：
斜率场线素的数量增加了一点：
微分方程 y'=y（红色曲线）和真实解e^x (绿色曲线)
可以看到，两者吻合的还是比较好的。
二阶微分方程 y''=-y-y'/10 (初始条件y(0)=1,y'(0)=0)
（有阻尼振动）（处于欠阻尼状态）
用微分方程研究共振现象：
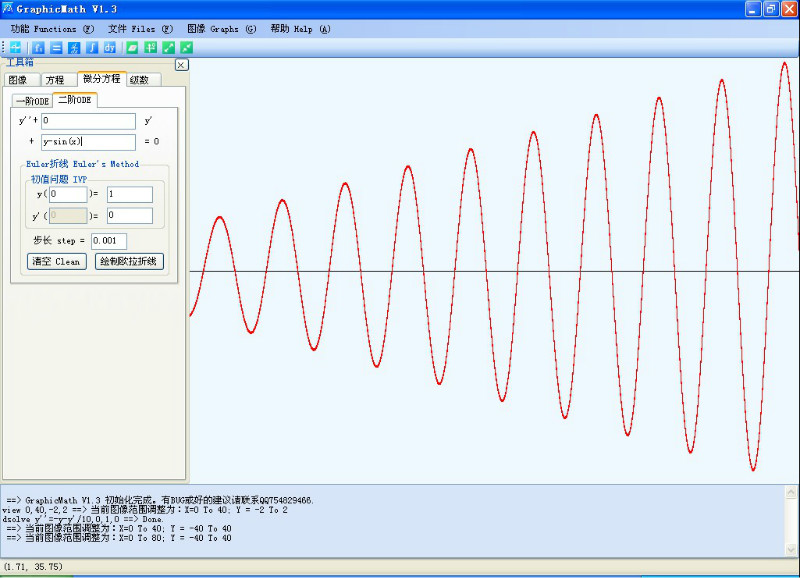
共振2：
泰勒级数：
自由振动方程：y''+y=0 (初始条件y(0)=1,y'(0)=0)
（欧拉折线法是红色曲线） 真实解为cos(x) （蓝色曲线）
这里步长为0.001
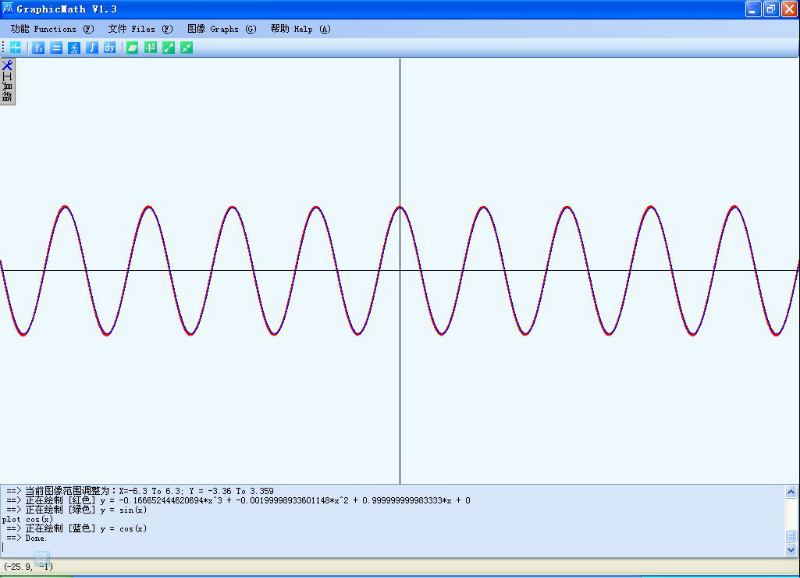
现在说明一下误差问题：【欧拉折线法具有一定误差，尤其是较快的振动或所谓的“刚性方程”】，而且步长越小误差也越小，只是计算量更大。
在版本(V1.4Beta)中，我们已经使用【龙格库塔方法】取代【欧拉折线法】。【龙格库塔方法】兼具有更高的精确度和比较不错的速度。
|
QQ好友和群
QQ空间
腾讯微博
腾讯朋友
收藏
淘帖
顶
踩
