- 实验目的:
- 通过虚拟仿真,观察平行板电容器与加盖导体槽内部的电场分布。
- 学习用模拟法测量静电场的方法。
 - 了解影响实验精度的因素。
- 实验装置
被测模型有两个:一个用来模拟无边缘效应的平行板电容器中的电位分布;另一个用来模拟有金属盖的无限长接地槽形导体内电位分布。被模拟的平行板电容器,加盖槽形导体及它们对应的模型如图1所示。  
图1 被测模型是在碳素导电纸上按所需的几何形状,尺寸制成如图1所示的金属“电极”。为保证各被测点位置,采用“网格板”来定位。该“网格板”是用透明塑料薄板,板上沿X、Y坐标轴每一厘米打一个小孔,这样就形成了一个正方形网格阵。 对于复杂边界的静电场边值问题,用解析法求解很困难,甚至是不可能的。在实际求解过程中,直接求出静电场的分布或电位又很困难,其精度也难以保证。本实验根据静电场与恒定电流场的相似性,用碳素导电纸中形成的恒定电流场来模拟无源区域的二维静电场,从而测出边界比较复杂的无源区域静电场分布。 在静电场的无源区域中,电场强度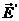 电位移矢量 电位移矢量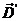 及电位 及电位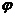 满足下列方程: 满足下列方程: 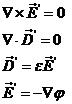 \* MERGEFORMAT (1) \* MERGEFORMAT (1) 式中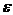 为静电场的介电常数。 为静电场的介电常数。 在恒定电流场中,电场强度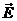 、电流密度 、电流密度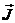 及电位 及电位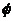 满足下列方程: 满足下列方程: 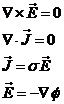 \* MERGEFORMAT (2) \* MERGEFORMAT (2) 式中 为恒定电流场中导电媒质的电导率。 为恒定电流场中导电媒质的电导率。 因为方程组(1)与方程组(2)在形式上完全相似,所以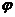 (静电场中的电位分布函数)与 (静电场中的电位分布函数)与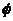 (恒定电流场中的电位分布函数)应满足同样形式的微分方程。由方程组(1)和方程组(2)很容易求得: (恒定电流场中的电位分布函数)应满足同样形式的微分方程。由方程组(1)和方程组(2)很容易求得:  \* MERGEFORMAT (3) \* MERGEFORMAT (3) 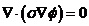 \* MERGEFORMAT (4) \* MERGEFORMAT (4) 式中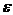 与 与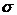 处于相应的位置,它们为对偶量。 处于相应的位置,它们为对偶量。 若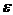 与 与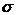 在所讨论区域为均匀分布(即其值与坐标无关),则方程(3)、(4)均可简化为拉普拉斯方程: 在所讨论区域为均匀分布(即其值与坐标无关),则方程(3)、(4)均可简化为拉普拉斯方程: 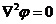 \* MERGEFORMAT (1.5) \* MERGEFORMAT (1.5) 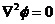 \* MERGEFORMAT (1.6) \* MERGEFORMAT (1.6) 电位场解的唯一定理可知:满足相同微分方程的两个电位场,它们具有相同的边界电位值,因此,在保证边界电位值不变的情况下,我们可以用恒定电流场的模型来模拟无源区域的静电场,当静电场中媒质为均匀媒质时,其导电媒质也应为均匀媒质,这样测得的恒定电流场的电位分布就是被模拟的静电场的电位分布,不需要任何改动。 Part A 虚拟仿真平行板电容器与加盖导体槽内的电位分布 使用Matlab或其它编程语言,编写程序,对被测模型的电位分布进行仿真。
- 自选仿真软件,自行设定参数,建立模型,对平行板电容器的电位分布进行虚拟仿真,观察平行板电容器的电位分布趋势,并将仿真结果图记录到实验报告。
- 自选仿真软件,自行设定参数,建立模型,对加盖导体槽内部的电位分布进行虚拟仿真,观察加盖导体槽内部的电位分布趋势,并将仿真结果图记录到实验报告。
- 将程序代码及相应的说明文字和图形附到实验报告的附录中,不够可附页。可以使用Matlab的pdetool工具箱,利用其图形化界面进行简单设置即可实现建模仿真,请将其设置参数截图与步骤说明记录到附录中。
- 实验数据:
Part A 虚拟仿真平行板电容器与加盖导体槽内的电位分布 设两个平行板放在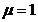 , ,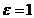 的环境中,导体板厚度为0.1,间距为1,长度为1,左侧导体板的电位为10V,右侧导体板的电位为-10V,无限远处空间电位为0V,初始条件满足狄利克雷条件。电位分布的仿真结果如下: 的环境中,导体板厚度为0.1,间距为1,长度为1,左侧导体板的电位为10V,右侧导体板的电位为-10V,无限远处空间电位为0V,初始条件满足狄利克雷条件。电位分布的仿真结果如下: 
由仿真结果可以看到,导体板间的电场强度可近似看作匀强电场,电位分布也可以近似为从左向右均匀下降。 设加盖导体槽放在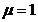 , ,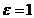 的环境中,盖板和槽壁的厚度均为0.1,盖板的宽度为1,导体槽的宽度为1,深度为1。初始条件为:盖板电位10V,导体槽接地,空间无限远处电位0V,满足狄利克雷条件。电位分布的仿真结果如下: 的环境中,盖板和槽壁的厚度均为0.1,盖板的宽度为1,导体槽的宽度为1,深度为1。初始条件为:盖板电位10V,导体槽接地,空间无限远处电位0V,满足狄利克雷条件。电位分布的仿真结果如下: 
从仿真结果可以看到,等位线密度由槽底中央向槽壁和盖板连接处逐渐变密。
附录: 请在此处附上虚拟仿真程序代码及其他需要附录的文字说明或图,可附页。 一. >>pdetool 1.画两个平行板:R1 R2和介质 R3: 
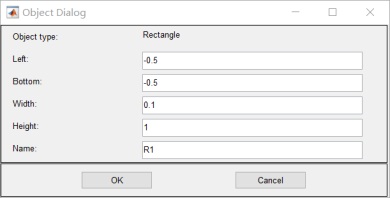 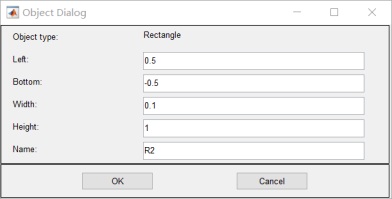 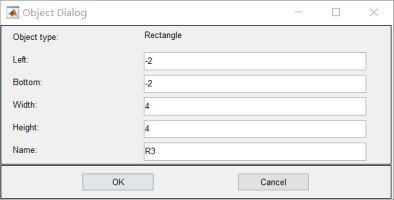


介质边界为0,左边电极板为10v,右面电极板为-10v: 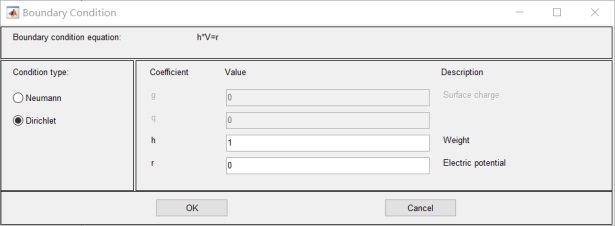
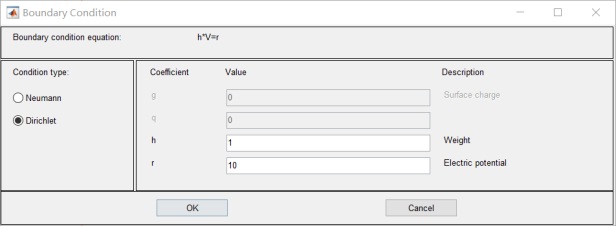
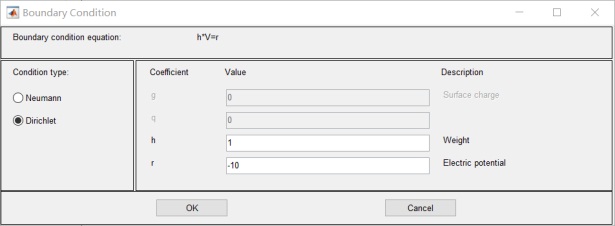
- 设置PDE 介质参数:epsilon=1;rho=0:
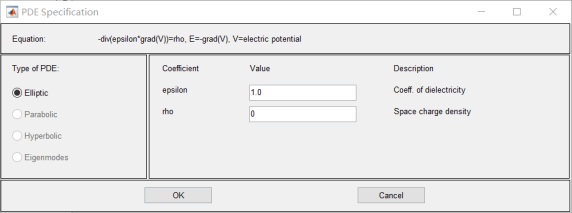
勾选contour和Arrows: 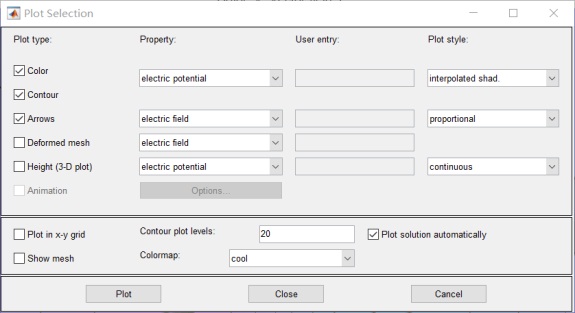
- pdetool 打开界面
- 画加盖导体槽:R1 R2 R3 R4 ,R4 是盖, 画介质R5:
 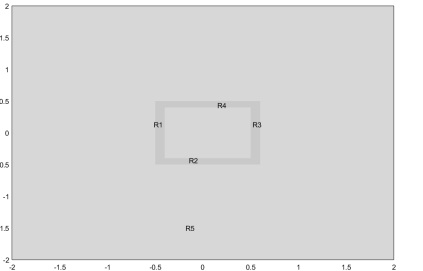
3.设置参数: 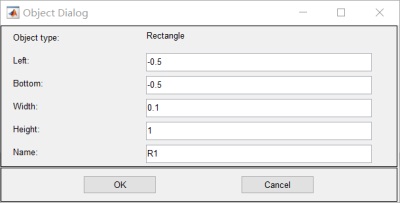
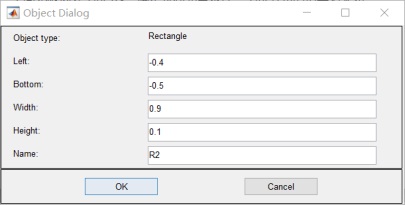
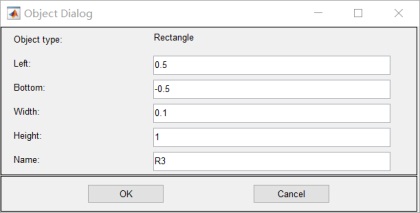 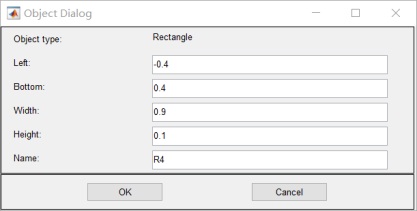 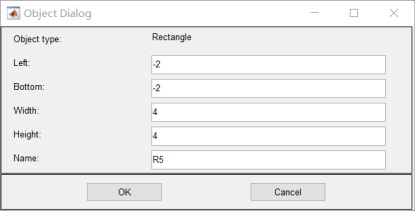
4.函数方程改为: 5. 将所求类型改为: 
6.设置边界值:其中R1 R2 R3 电位为0;R4 为10v 无穷远为0v:  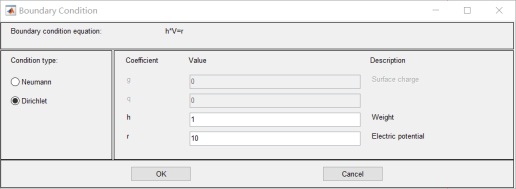 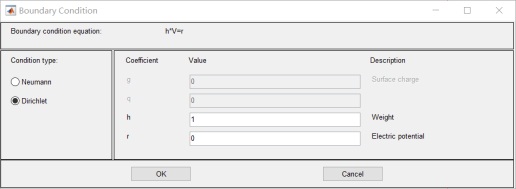
7.设置 介质参数: 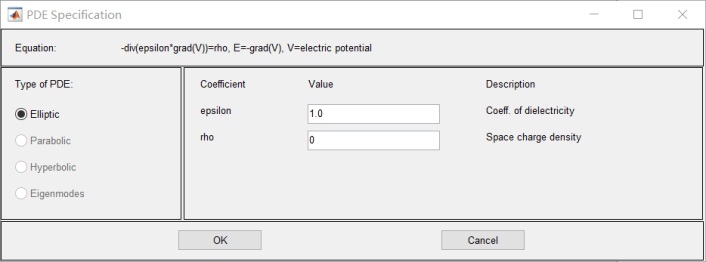
8.画图: 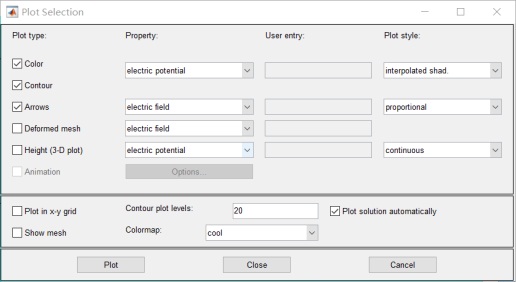
完整的Word格式文档51黑下载地址:
 静电场边值问题研究实验.docx
(786.33 KB, 下载次数: 3)
静电场边值问题研究实验.docx
(786.33 KB, 下载次数: 3)
|