LMI算法设计状态反馈H∞控制器的一个例子

ID:77367 · 发表于 2015-4-18 20:32

这两天看到很多关于线性矩阵不等式（Linear MatrixInequality，LMI）算法方面的东西，但是好像没一个实际的例子可以参考，纠结了两天做了一个单级倒立摆的例子出来，对有些人说不定还是有用的，PS：这是我毕业论文的一部分

。
一个倒立摆系统的数学模型转化成标准的H∞控制问题模型，即：

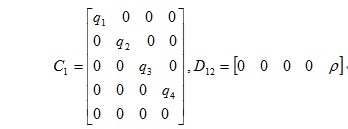给加权矩阵C1和D12选择一个合适的参数（通常是通过仿真反复试验得出来），求解下面的一个LMI，使γ的值取到最小，从而得到一个最优的

态反馈H∞控制器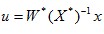

。

下面是利用MATLAB LMI工具箱解决这个问题独一无二的例子，网上没有第二份这样的代码了。另外仿真还可以使用MATLAB/Simulink。。。。。

%基于LMI算法的倒立摆状态反馈H∞控制器设计
%State Feedback H∞ controller design based lmi approach
%by 2013/04/03 hemmingway <hemmingway@163.com>

clc
clear all
%----------------------------------------------%
%定义常数矩阵
A=[0  1    0    0;
0 -0.0883  0.6293  0;
0  0    0    1;
0 -0.2357  27.8285 0] ;
B1=[0 2.3566  0 104.2027]';
B2=[0 0.8832  0 2.3566]';
C1=[0.064 0 0 0;
0    1e-3  0 0;
0    0 0.11 0;
0    0 0 0.01;
0    0 0 0];
D12=[0 0 0 0 0.01]';
D11=[0 0 0 0 0]';
C2=[1 0 0 0;
0 0 1 0];
D21=[0 0 0 0]';
D22=[0 0 0 0]';

%
setlmis([]);    %建立一个LMI
X=lmivar(1,[4,1]); %定义矩阵变量
W=lmivar(2,[1,4]);
r1=lmivar(1,[1,1]);

%%%%%%%
lmiterm([1 1 1 X],A,1,'s');
lmiterm([1 1 1 W],B2,1,'s');
lmiterm([1 2 1 0],B1');
lmiterm([1 2 2 0],-1);
lmiterm([1 3 1 X],C1,1);
lmiterm([1 3 1 W],D12,1);
lmiterm([1 3 2 0],D11);
lmiterm([1 3 3 r1],-1,1);

%
lmiterm([-2 1 1 X],1,1);

lmisys=getlmis;

%%----------------------------solver---------------------------------------
n = decnbr(lmisys);
c = zeros(n,1);
for j=1:n
   [r1j]=defcx(lmisys,j,r1);
   c(j)=trace(r1j);
end
%c=mat2dec(lmisys,zeros(4,4),zeros(1,4),eye(1))
[copt,xopt]=mincx(lmisys,c, [0 0 0 0 0]);

X=dec2mat(lmisys,xopt,X)
W=dec2mat(lmisys,xopt,W)

K=W*X^(-1);
K=K/100 %%控制器,为什么要除以100？因为D12矩阵哪里是0.001,不是传统的1

r1=dec2mat(lmisys,xopt,r1);
gammar=r1^(1/2)             %%gammar

%----------------------------------simu------------------------------------
%
w=0.0;
n=1;
Dt=0.01;
t=-0.8;
t0=t;
x=[-0.2 0 0.3 0]';
for i=1:1500
   if t<0
      %t1=4*pi*t;
      t1=4*pi*t;
      x=[1.1*sin(t1); 1.2*cos(t1); 0.5*sin(t1)+1.0*cos(t1); 0];
else
   u=K*x;                   %%反馈控制
   Dx=A*x+B1*w+B2*u;
   x=x+Dx*Dt;
end

Y(:,n)=x;
t=t+Dt;
n=n+1;
end

figure(1)
time = (1:n-1)*Dt+t0;
xpos=Y(1,:);
xangle=Y(3,:);

subplot(2,1,1)
plot((1:n-1)*Dt+t0,xpos,'k')
axis([-0.8 10 -1.5 1.5])
grid on
xlabel('time(s)')
ylabel('Cart positon')

subplot(2,1,2)
plot((1:n-1)*Dt+t0,xangle,'k')
axis([-0.8 10 -1.5 1.5])
grid on
xlabel('time(s)')
ylabel('Pendulum')